তাপগতিবিদ্যার দৃষ্টিকোণ থেকে গ্যাসগুলিকে ম্যাক্রোস্কোপিক বৈশিষ্ট্যের একটি সেট দ্বারা বর্ণনা করা হয়, যার মধ্যে প্রধান হল তাপমাত্রা, চাপ এবং আয়তন। এই পরামিতিগুলির একটির স্থায়িত্ব এবং অন্য দুটির পরিবর্তন ইঙ্গিত করে যে গ্যাসে এক বা অন্য আইসোপ্রসেস ঘটে। আমরা এই নিবন্ধটি এই প্রশ্নগুলির একটি বিশদ উত্তরের জন্য উত্সর্গ করব যে এটি একটি আইসোকোরিক প্রক্রিয়া, এটি কীভাবে একটি গ্যাস সিস্টেমের রাজ্যে আইসোথার্মাল এবং আইসোবারিক পরিবর্তনগুলির থেকে আলাদা৷
পদার্থবিদ্যায় আদর্শ গ্যাস

এটি একটি আইসোকোরিক প্রক্রিয়া যে প্রশ্নের উত্তর দেওয়ার আগে, আপনাকে একটি আদর্শ গ্যাসের ধারণাটি আরও ভালভাবে জানতে হবে। পদার্থবিজ্ঞানে, এটিকে এমন কোনো গ্যাস হিসাবে বোঝা যায় যেখানে এর উপাদান কণাগুলির গড় গতিশক্তি তাদের মিথস্ক্রিয়ার সম্ভাব্য শক্তিকে ছাড়িয়ে যায় এবং এই কণাগুলির মধ্যকার দূরত্বগুলি তাদের রৈখিক মাত্রার চেয়ে অনেক বেশি মাত্রার। উল্লিখিত অবস্থার অধীনে, এটি সম্ভব, যখন আউট বহনগণনাগুলি কণাগুলির মধ্যে মিথস্ক্রিয়া শক্তিকে বিবেচনা করে না (এটি শূন্যের সমান), এবং এটিও অনুমান করা যেতে পারে যে কণাগুলি একটি নির্দিষ্ট ভরের বস্তুগত বিন্দু।
একটি আদর্শ গ্যাসে সঞ্চালিত একমাত্র প্রক্রিয়াটি হল পদার্থ ধারণকারী জাহাজের দেয়ালের সাথে কণার সংঘর্ষ। এই সংঘর্ষগুলি অনুশীলনে P গ্যাসে একটি নির্দিষ্ট চাপের অস্তিত্ব হিসাবে নিজেকে প্রকাশ করে।
একটি নিয়ম হিসাবে, যে কোনো গ্যাসীয় পদার্থ যা তুলনামূলকভাবে রাসায়নিকভাবে নিষ্ক্রিয় অণু নিয়ে গঠিত এবং যার নিম্নচাপ এবং উচ্চ তাপমাত্রা আছে তা ব্যবহারিক গণনার জন্য পর্যাপ্ত নির্ভুলতার সাথে একটি আদর্শ গ্যাস হিসাবে বিবেচিত হতে পারে।
একটি আদর্শ গ্যাস বর্ণনাকারী সমীকরণ
অবশ্যই, আমরা Clapeyron-Mendeleev এর সার্বজনীন আইন সম্পর্কে কথা বলছি, যেটি একটি আইসোকোরিক প্রক্রিয়া বোঝার জন্য এটিকে ভালভাবে বোঝা উচিত। সুতরাং, রাষ্ট্রের সর্বজনীন সমীকরণের নিম্নলিখিত রূপ রয়েছে:
PV=nRT.
অর্থাৎ, চাপ P এবং গ্যাসের আয়তন V এর গুণফল পরম তাপমাত্রা T এর গুণফল এবং মোল n-এ পদার্থের পরিমাণের সমান, যেখানে R হল আনুপাতিকতা ফ্যাক্টর। সমীকরণটি নিজেই 1834 সালে এমিল ক্ল্যাপেইরন প্রথম লিখেছিলেন এবং 19 শতকের 70 এর দশকে, ডি. মেন্ডেলিভ এটিতে একটি একক সর্বজনীন গ্যাস ধ্রুবক R (8.314 J/(molK) এর ধ্রুবক মানের একটি সেট প্রতিস্থাপিত করেছিলেন))।
ক্লেপেয়ারন-মেন্ডেলিভ সমীকরণ অনুসারে, একটি বদ্ধ সিস্টেমে গ্যাস কণার সংখ্যা স্থির থাকে, তাই শুধুমাত্র তিনটি ম্যাক্রোস্কোপিক প্যারামিটার রয়েছে যা পরিবর্তন করতে পারে (T, Pএবং ভি)। পরবর্তী ঘটনাটি বিভিন্ন আইসোপ্রসেসগুলির বোঝার অন্তর্নিহিত যা নীচে আলোচনা করা হবে৷
আইসোকোরিক প্রক্রিয়া কি?
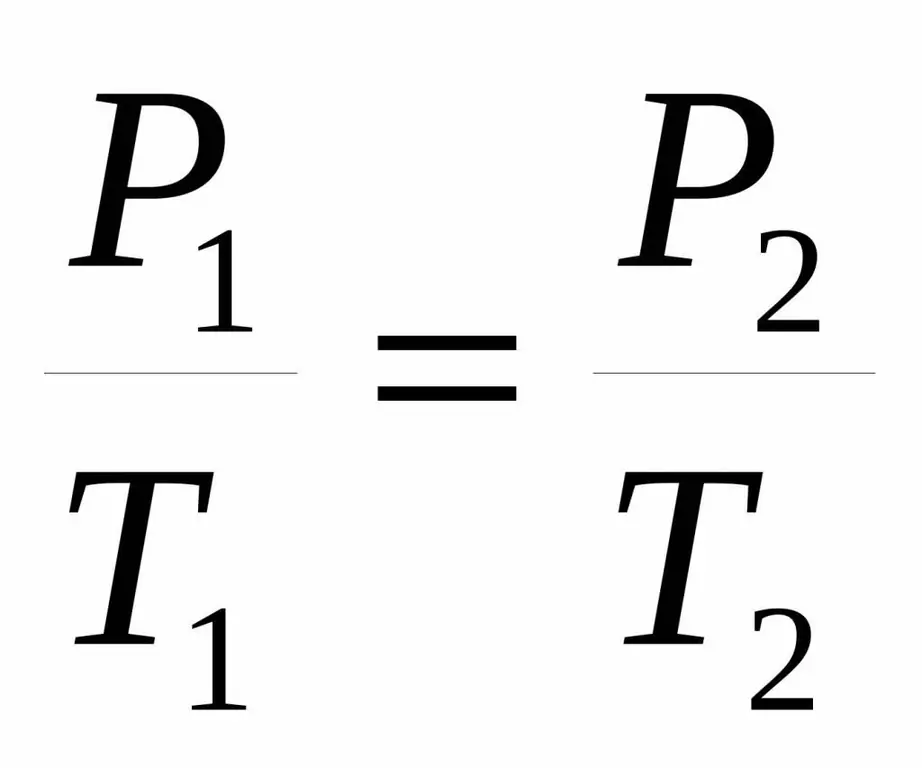
এই প্রক্রিয়াটিকে সিস্টেমের অবস্থার যে কোনও পরিবর্তন হিসাবে বোঝা যায়, যেখানে এর আয়তন সংরক্ষিত থাকে।
যদি আমরা রাষ্ট্রের সার্বজনীন সমীকরণের দিকে ফিরে যাই, আমরা বলতে পারি যে একটি আইসোকোরিক প্রক্রিয়ায় একটি গ্যাসে শুধুমাত্র চাপ এবং পরম তাপমাত্রা পরিবর্তন হয়। থার্মোডাইনামিক পরামিতিগুলি ঠিক কীভাবে পরিবর্তিত হয় তা বোঝার জন্য, আমরা সংশ্লিষ্ট গাণিতিক অভিব্যক্তি লিখি:
P / T=consst.
কখনও কখনও এই সমতা একটু ভিন্ন আকারে দেওয়া হয়:
P1 / T1=P2 / T 2.
উভয় সমতাকে একজন ফরাসি বিজ্ঞানীর নাম অনুসারে চার্লসের আইন বলা হয় যিনি 18 শতকের শেষের দিকে পরীক্ষামূলকভাবে উল্লেখযোগ্য নির্ভরতা অর্জন করেছিলেন।

যদি আমরা P(T) ফাংশনের একটি গ্রাফ তৈরি করি, তাহলে আমরা একটি সরল-রেখা নির্ভরতা পাব, যাকে বলা হয় আইসোকোর। যেকোনো আইসোকোর (n এবং V এর সমস্ত মানের জন্য) একটি সরল রেখা।
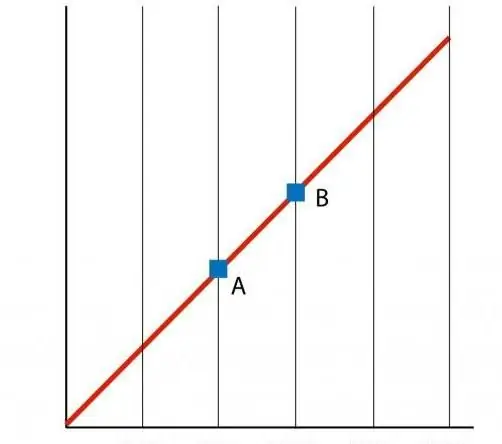
প্রক্রিয়াটির শক্তি বিবরণ
উল্লেখ্য হিসাবে, একটি আইসোকোরিক প্রক্রিয়া হল একটি সিস্টেমের অবস্থার পরিবর্তন যা একটি বন্ধ কিন্তু বিচ্ছিন্ন সিস্টেমে ঘটে না। আমরা গ্যাস এবং পরিবেশের মধ্যে তাপ বিনিময়ের সম্ভাবনা সম্পর্কে কথা বলছি। সাধারণভাবে, সিস্টেমে তাপ Q সরবরাহ দুটি ফলাফলের দিকে পরিচালিত করে:
- অভ্যন্তরীণ শক্তি U পরিবর্তন করে;
- গ্যাসA, সম্প্রসারণ বা চুক্তির কাজ করে।
শেষ অনুমানটি গাণিতিকভাবে নিম্নরূপ লেখা হয়েছে:
Q=U + A.
একটি আদর্শ গ্যাসের আইসোকোরিক প্রক্রিয়া, এর সংজ্ঞা অনুসারে, গ্যাস দ্বারা সম্পন্ন কাজ বোঝায় না, যেহেতু এর আয়তন অপরিবর্তিত থাকে। এর মানে হল যে সিস্টেমে সরবরাহ করা সমস্ত তাপ তার অভ্যন্তরীণ শক্তি বাড়াতে যায়:
Q=U.
যদি আমরা এই অভিব্যক্তিতে অভ্যন্তরীণ শক্তির সুস্পষ্ট সূত্র প্রতিস্থাপন করি, তাহলে আইসোকোরিক প্রক্রিয়ার তাপকে এইভাবে উপস্থাপন করা যেতে পারে:
Q=z / 2nRT.
এখানে z হল স্বাধীনতার ডিগ্রির সংখ্যা, যা গ্যাস তৈরিকারী অণুগুলির পলিআটমিক প্রকৃতির দ্বারা নির্ধারিত হয়। একটি মোনাটমিক গ্যাসের জন্য, z=3, একটি ডায়াটমিক গ্যাসের জন্য - 5, এবং একটি ট্রায়াটমিক এবং আরও অনেকের জন্য - 6। এখানে, স্বাধীনতার ডিগ্রির অধীনে, আমরা অনুবাদমূলক এবং ঘূর্ণনগত ডিগ্রী বলতে চাই।
যদি আমরা আইসোকোরিক এবং আইসোবারিক প্রক্রিয়াগুলিতে একটি গ্যাস সিস্টেম গরম করার দক্ষতা তুলনা করি, তবে প্রথম ক্ষেত্রে আমরা সর্বাধিক দক্ষতা পাব, যেহেতু সিস্টেমের অবস্থার আইসোবারিক পরিবর্তনের সময়, গ্যাস প্রসারিত হয় এবং তাপ ইনপুটের একটি অংশ কাজে ব্যয় করা হয়৷
আইসোবারিক প্রক্রিয়া
উপরে আমরা বিস্তারিত বর্ণনা করেছি যে এটি একটি আইসোকোরিক প্রক্রিয়া। এখন আসুন অন্যান্য আইসোপ্রসেস সম্পর্কে কিছু কথা বলি। আইসোবারিক দিয়ে শুরু করা যাক। নামের উপর ভিত্তি করে, এটি ধ্রুবক চাপে রাজ্যগুলির মধ্যে সিস্টেমের রূপান্তর হিসাবে বোঝা যায়। এই প্রক্রিয়াটি গে-লুসাক আইন দ্বারা নিম্নরূপ বর্ণনা করা হয়েছে:
V / T=consst.
আইসোকোরের মতো, ভি(টি) আইসোবারও গ্রাফে একটি সরল রেখাকে প্রতিনিধিত্ব করে।
এর জন্যযেকোন আইসোবারিক প্রক্রিয়ার জন্য, গ্যাস দ্বারা সম্পন্ন কাজটি গণনা করা সুবিধাজনক, কারণ এটি ধ্রুবক চাপের গুণফল এবং আয়তনের পরিবর্তনের সমান।
আইসোথার্মাল প্রক্রিয়া
এটি এমন একটি প্রক্রিয়া যেখানে সিস্টেমের তাপমাত্রা স্থির থাকে। এটি একটি আদর্শ গ্যাসের জন্য বয়েল-মেরিওট আইন দ্বারা বর্ণনা করা হয়েছে। এটি লক্ষ্য করা কৌতূহলী যে এটি প্রথম পরীক্ষামূলকভাবে আবিষ্কৃত গ্যাস আইন (17 শতকের দ্বিতীয়ার্ধ)। এর গাণিতিক স্বরলিপি এইরকম দেখায়:
PV=const.
আইসোকোরিক এবং আইসোথার্মাল প্রক্রিয়াগুলি তাদের গ্রাফিকাল উপস্থাপনার পরিপ্রেক্ষিতে পৃথক, যেহেতু ফাংশন P(V) একটি হাইপারবোলিক, একটি রৈখিক সম্পর্ক নয়৷
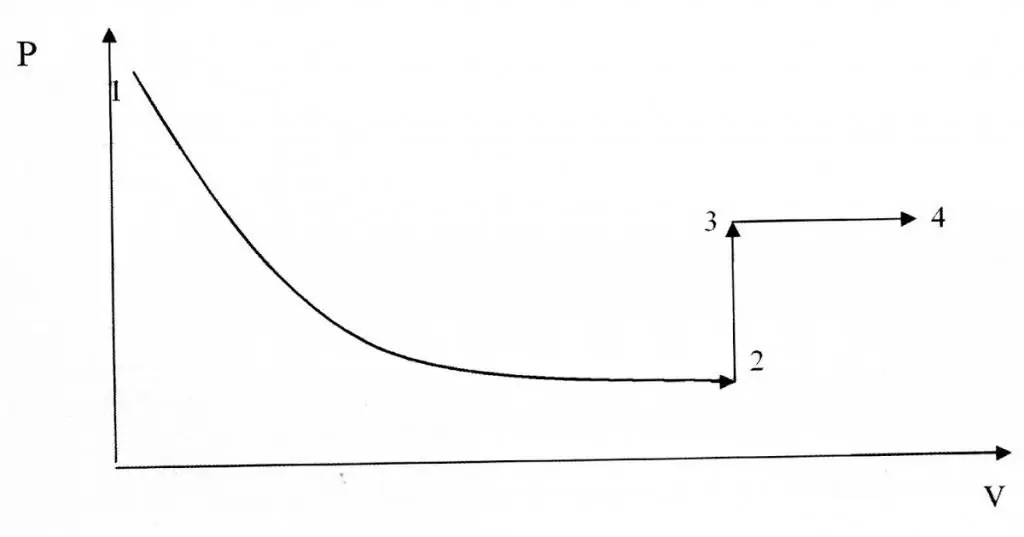
সমস্যা সমাধানের উদাহরণ
আসুন একটি ব্যবহারিক সমস্যা সমাধানের জন্য তাদের আবেদনের মাধ্যমে নিবন্ধে প্রদত্ত তাত্ত্বিক তথ্যকে একীভূত করি। এটি জানা যায় যে বিশুদ্ধ বায়বীয় নাইট্রোজেন একটি সিলিন্ডারে 1 বায়ুমণ্ডলের চাপ এবং 25 ডিগ্রি সেলসিয়াস তাপমাত্রায় ছিল। গ্যাস সিলিন্ডারটি গরম করার পরে এবং এতে চাপ পরিমাপ করা হয়, এটি 1.5 বায়ুমণ্ডল হিসাবে পরিণত হয়। গরম করার পর সিলিন্ডারে গ্যাসের তাপমাত্রা কত হয়? বেলুনে নাইট্রোজেনের 4 টি মোল থাকলে গ্যাসের অভ্যন্তরীণ শক্তি কত পরিমাণে পরিবর্তিত হয়।
প্রথম প্রশ্নের উত্তর দিতে, আমরা নিম্নলিখিত অভিব্যক্তি ব্যবহার করি:
P1 / T1=P2 / T 2.
যেখান থেকে আমরা পাই:
T2=P2 / P1 T 1.
এই অভিব্যক্তিতে, চাপকে নির্বিচারে এককে প্রতিস্থাপিত করা যেতে পারেপরিমাপ, যেহেতু তারা সঙ্কুচিত হচ্ছে, এবং তাপমাত্রা শুধুমাত্র কেলভিনে। এই বলে, আমরা পাই:
T2=1.5 /1298.15=447.224 K.
ডিগ্রী সেলসিয়াসে গণনা করা তাপমাত্রা হল 174 °C।
যেহেতু নাইট্রোজেন অণু ডায়াটমিক, তাই গরম করার সময় এর অভ্যন্তরীণ শক্তির পরিবর্তন নিম্নরূপ নির্ধারণ করা যেতে পারে:
ΔU=5 / 2nRΔT.
এই অভিব্যক্তিতে পরিচিত মানগুলিকে প্রতিস্থাপন করলে, আমরা সমস্যার দ্বিতীয় প্রশ্নের উত্তর পাব: ΔU=+12.4 kJ.






