প্রতিটি ব্যক্তি তার জীবনের সময় এমন দেহের মুখোমুখি হয় যা পদার্থের তিনটি সামগ্রিক অবস্থার একটিতে থাকে। অধ্যয়নের জন্য একত্রিতকরণের সহজতম অবস্থা হল গ্যাস। নিবন্ধে, আমরা একটি আদর্শ গ্যাসের ধারণা বিবেচনা করব, সিস্টেমের অবস্থার সমীকরণ দেব এবং পরম তাপমাত্রার বর্ণনার দিকেও কিছু মনোযোগ দেব।
গ্যাসের পদার্থের অবস্থা
প্রত্যেক শিক্ষার্থীর ভালো ধারণা থাকে যে তারা "গ্যাস" শব্দটি শুনলে তারা কোন পদার্থের বিষয়ে কথা বলছে। এই শব্দটি এমন একটি শরীর হিসাবে বোঝা যায় যা এটিকে দেওয়া যে কোনও ভলিউম দখল করতে সক্ষম। এটি তার আকৃতি রাখতে সক্ষম নয়, কারণ এটি সামান্যতম বাহ্যিক প্রভাবকেও প্রতিরোধ করতে পারে না। এছাড়াও, গ্যাস ভলিউম ধরে রাখে না, যা এটিকে শুধুমাত্র কঠিন পদার্থ থেকে নয়, তরল থেকেও আলাদা করে।
তরলের মতোই গ্যাসও একটি তরল পদার্থ। গ্যাসে কঠিন বস্তুর গতির প্রক্রিয়ায়, পরেরটি এই গতিকে বাধা দেয়। ফলস্বরূপ শক্তিকে প্রতিরোধ বলে। এর মান নির্ভর করেগ্যাসে শরীরের বেগ।
গ্যাসের শক্তিশালী উদাহরণ হল বায়ু, ঘর গরম করা এবং রান্নার জন্য ব্যবহৃত প্রাকৃতিক গ্যাস, জড় গ্যাস (Ne, Ar) বিজ্ঞাপনের গ্লো টিউবগুলি পূরণ করতে বা ঢালাই করার সময় একটি নিষ্ক্রিয় (অ-আক্রমনাত্মক, প্রতিরক্ষামূলক) পরিবেশ তৈরি করতে ব্যবহৃত হয়।.
আদর্শ গ্যাস
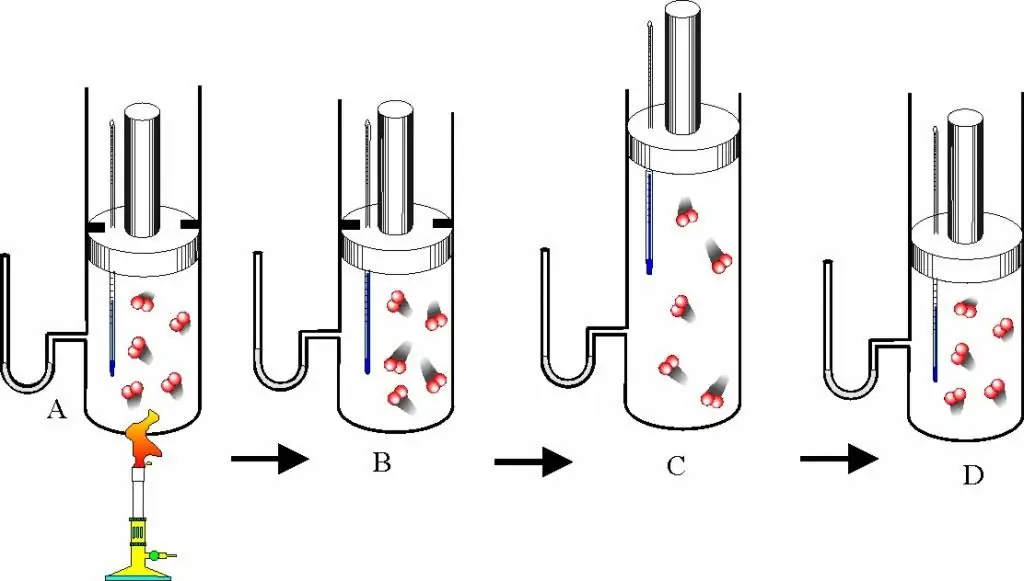
গ্যাস আইন এবং রাষ্ট্রের সমীকরণের বর্ণনায় এগিয়ে যাওয়ার আগে, আপনার একটি আদর্শ গ্যাস কী সেই প্রশ্নটি ভালোভাবে বুঝতে হবে। এই ধারণাটি আণবিক গতি তত্ত্বে (MKT) চালু করা হয়েছে। একটি আদর্শ গ্যাস হল যে কোনো গ্যাস যা নিম্নলিখিত বৈশিষ্ট্যগুলিকে সন্তুষ্ট করে:
- যান্ত্রিক সংঘর্ষ ছাড়া যে কণাগুলি এটি তৈরি করে তারা একে অপরের সাথে যোগাযোগ করে না।
- যানের দেয়ালের সাথে বা নিজেদের মধ্যে কণার সংঘর্ষের ফলে তাদের গতিশক্তি এবং ভরবেগ সংরক্ষিত হয়, অর্থাৎ সংঘর্ষকে একেবারে স্থিতিস্থাপক বলে মনে করা হয়।
- কণার কোনো মাত্রা নেই, তবে তাদের একটি সীমিত ভর রয়েছে, অর্থাৎ তারা বস্তুগত বিন্দুর মতো।
এটা স্বাভাবিক যে কোনো গ্যাস আদর্শ নয়, কিন্তু বাস্তব। তবুও, অনেক ব্যবহারিক সমস্যা সমাধানের জন্য, এই অনুমানগুলি বেশ বৈধ এবং ব্যবহার করা যেতে পারে। একটি সাধারণ অভিজ্ঞতামূলক নিয়ম রয়েছে যা বলে: রাসায়নিক প্রকৃতির নির্বিশেষে, যদি একটি গ্যাসের তাপমাত্রা ঘরের তাপমাত্রার উপরে থাকে এবং বায়ুমণ্ডলীয় বা নিম্নের ক্রম অনুসারে চাপ থাকে, তবে এটি উচ্চ নির্ভুলতার সাথে আদর্শ হিসাবে বিবেচিত হতে পারে এবং বর্ণনা করতে ব্যবহার করা যেতে পারে। এটারাষ্ট্রের আদর্শ গ্যাস সমীকরণের সূত্র।
ক্লেপিরন-মেন্ডেলিভ আইন
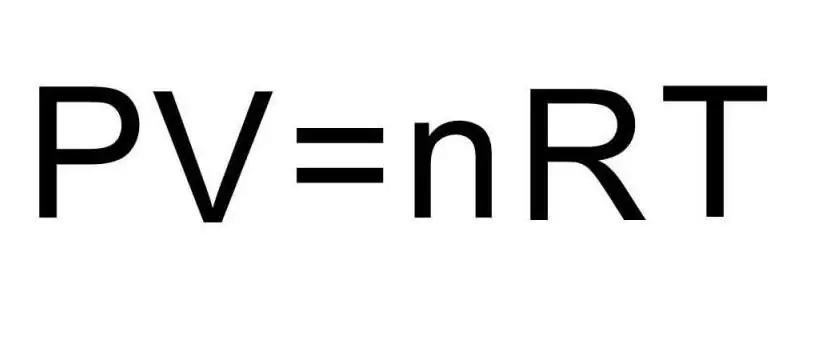
পদার্থের বিভিন্ন সমষ্টিগত অবস্থার মধ্যে স্থানান্তর এবং একটি একক সামগ্রিক অবস্থার মধ্যে প্রক্রিয়াগুলি তাপগতিবিদ্যা দ্বারা পরিচালিত হয়। চাপ, তাপমাত্রা এবং আয়তন তিনটি পরিমাণ যা একটি থার্মোডাইনামিক সিস্টেমের যেকোনো অবস্থাকে স্বতন্ত্রভাবে সংজ্ঞায়িত করে। একটি আদর্শ গ্যাসের অবস্থার সমীকরণের সূত্রটি এই তিনটি পরিমাণকে একক সমতায় যুক্ত করে। আসুন এই সূত্রটি লিখি:
PV=nRT
এখানে যথাক্রমে P, V, T - চাপ, আয়তন, তাপমাত্রা। n-এর মান হল মোলে পদার্থের পরিমাণ এবং R চিহ্নটি গ্যাসের সর্বজনীন ধ্রুবককে নির্দেশ করে। এই সমতা দেখায় যে চাপ এবং আয়তনের গুণফল যত বেশি হবে, পদার্থ এবং তাপমাত্রার পরিমাণের গুণফল তত বেশি হবে।

গ্যাসের অবস্থার সমীকরণের সূত্রটিকে ক্ল্যাপেয়ারন-মেন্ডেলিভ সূত্র বলা হয়। 1834 সালে, ফরাসি বিজ্ঞানী এমিল ক্ল্যাপেয়ারন, তার পূর্বসূরিদের পরীক্ষামূলক ফলাফলের সংক্ষিপ্তসার এই সমীকরণে এসেছিলেন। যাইহোক, ক্ল্যাপেইরন অনেকগুলি ধ্রুবক ব্যবহার করেছিলেন, যা মেন্ডেলিভ পরে একটি দিয়ে প্রতিস্থাপিত করেছিলেন - সর্বজনীন গ্যাস ধ্রুবক R (8, 314 J / (molK))। অতএব, আধুনিক পদার্থবিদ্যায়, এই সমীকরণের নামকরণ করা হয়েছে ফরাসি এবং রাশিয়ান বিজ্ঞানীদের নামের উপর।

অন্যান্য সমীকরণ ফর্ম
উপরে, আমরা একটি আদর্শ গ্যাসের জন্য রাষ্ট্রের মেন্ডেলিভ-ক্ল্যাপেয়ারন সমীকরণ লিখেছি যা সাধারণভাবে গৃহীত এবংসুবিধাজনক ফর্ম। যাইহোক, তাপগতিবিদ্যার সমস্যায়, একটি সামান্য ভিন্ন ফর্ম প্রায়ই প্রয়োজন হতে পারে। নীচে আরও তিনটি সূত্র লেখা আছে, যা সরাসরি লিখিত সমীকরণ থেকে অনুসরণ করে:
PV=NkBT;
PV=m/MRT;
P=ρRT/M.
এই তিনটি সমীকরণ একটি আদর্শ গ্যাসের জন্যও সার্বজনীন, শুধুমাত্র তাদের মধ্যে ভর m, মোলার ভর M, ঘনত্ব ρ এবং সিস্টেমটি তৈরি করে N কণার সংখ্যার মতো পরিমাণ। kB এখানে বোল্টজম্যান ধ্রুবককে বোঝায় (1, 3810-23J/K)।
বয়েল-ম্যারিওট ল
ক্লেপিরন যখন তার সমীকরণ তৈরি করেছিলেন, তখন তিনি গ্যাস আইনের উপর ভিত্তি করে তৈরি করেছিলেন যা কয়েক দশক আগে পরীক্ষামূলকভাবে আবিষ্কৃত হয়েছিল। তাদের মধ্যে একটি বয়েল-ম্যারিওট আইন। এটি একটি বদ্ধ সিস্টেমে একটি আইসোথার্মাল প্রক্রিয়া প্রতিফলিত করে, যার ফলস্বরূপ চাপ এবং ভলিউম পরিবর্তনের মতো ম্যাক্রোস্কোপিক পরামিতিগুলি। যদি আমরা একটি আদর্শ গ্যাসের জন্য রাষ্ট্রের সমীকরণে T এবং n ধ্রুবক রাখি, তাহলে গ্যাসের সূত্রটি রূপ নেবে:
P1V1=P2V 2
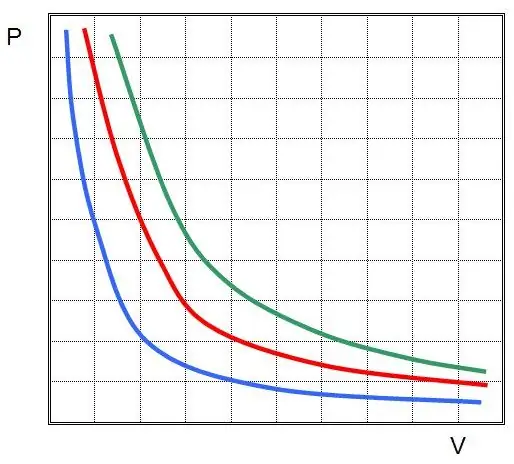
এটি বয়েল-ম্যারিওট আইন, যা বলে যে চাপ এবং আয়তনের গুণফল একটি নির্বিচারে আইসোথার্মাল প্রক্রিয়া চলাকালীন সংরক্ষিত থাকে। এই ক্ষেত্রে, P এবং V মানগুলি নিজেই পরিবর্তিত হয়।
যদি আপনি P(V) বা V(P) প্লট করেন, তাহলে আইসোথার্মগুলি হাইপারবোলাস হবে।
চার্লস এবং গে-লুসাকের আইন
এই আইনগুলি গাণিতিকভাবে আইসোবারিক এবং আইসোকোরিককে বর্ণনা করেপ্রক্রিয়াগুলি, অর্থাৎ, গ্যাস সিস্টেমের রাজ্যগুলির মধ্যে এই ধরনের রূপান্তর, যেখানে যথাক্রমে চাপ এবং আয়তন সংরক্ষিত হয়। চার্লসের আইনটি গাণিতিকভাবে নিম্নরূপ লেখা যেতে পারে:
V/T=const যখন n, P=const।
গে-লুসাকের আইনটি নিম্নরূপ লেখা হয়েছে:
P/T=const যখন n, V=const।
যদি উভয় সমতা একটি গ্রাফ আকারে উপস্থাপিত হয়, তাহলে আমরা সরল রেখা পাব যেগুলি x-অক্ষের কিছু কোণে ঝুঁকে আছে। এই ধরনের গ্রাফ স্থির চাপে আয়তন এবং তাপমাত্রার মধ্যে এবং ধ্রুব ভলিউমে চাপ এবং তাপমাত্রার মধ্যে একটি সরাসরি আনুপাতিকতা নির্দেশ করে।
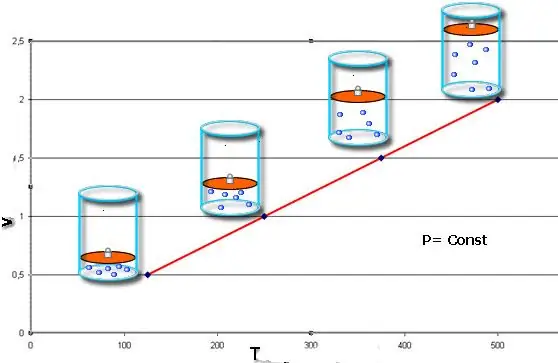
উল্লেখ্য যে তিনটি বিবেচিত গ্যাস আইনই গ্যাসের রাসায়নিক গঠন, সেইসাথে এর পদার্থের পরিমাণের পরিবর্তনকে বিবেচনা করে না।
পরম তাপমাত্রা
দৈনন্দিন জীবনে, আমরা সেলসিয়াস তাপমাত্রা স্কেল ব্যবহার করতে অভ্যস্ত, কারণ এটি আমাদের চারপাশের প্রক্রিয়াগুলি বর্ণনা করার জন্য সুবিধাজনক। সুতরাং, জল 100 oC তাপমাত্রায় ফুটতে থাকে এবং 0 oC তাপমাত্রায় জমে যায়। পদার্থবিজ্ঞানে, এই স্কেলটি অসুবিধাজনক বলে প্রমাণিত হয়, তাই তথাকথিত পরম তাপমাত্রা স্কেল, যা 19 শতকের মাঝামাঝি সময়ে লর্ড কেলভিন দ্বারা প্রবর্তিত হয়েছিল, ব্যবহৃত হয়। এই স্কেল অনুসারে, কেলভিন (কে) এ তাপমাত্রা পরিমাপ করা হয়।
এটা বিশ্বাস করা হয় যে -273, 15 oC তাপমাত্রায় পরমাণু এবং অণুগুলির কোনও তাপীয় কম্পন নেই, তাদের অগ্রগতি সম্পূর্ণভাবে বন্ধ হয়ে যায়। ডিগ্রি সেলসিয়াসে এই তাপমাত্রা কেলভিনের (0 কে) পরম শূন্যের সাথে মিলে যায়। এই সংজ্ঞা থেকেপরম তাপমাত্রার ভৌত অর্থ নিম্নরূপ: এটি পদার্থ তৈরি করে এমন কণার গতিশক্তির একটি পরিমাপ, উদাহরণস্বরূপ, পরমাণু বা অণু।
পরম তাপমাত্রার উপরোক্ত শারীরিক অর্থ ছাড়াও, এই পরিমাণ বোঝার জন্য অন্যান্য পদ্ধতি রয়েছে। তার মধ্যে একটি হল চার্লসের উল্লিখিত গ্যাস আইন। আসুন এটিকে নিম্নলিখিত আকারে লিখি:
V1/T1=V2/T 2=>
V1/V2=T1/T 2.
শেষ সমতা বলে যে সিস্টেমে পদার্থের একটি নির্দিষ্ট পরিমাণে (উদাহরণস্বরূপ, 1 মোল) এবং একটি নির্দিষ্ট চাপে (উদাহরণস্বরূপ, 1 Pa), গ্যাসের পরিমাণ স্বতন্ত্রভাবে পরম তাপমাত্রা নির্ধারণ করে। অন্য কথায়, এই অবস্থার অধীনে গ্যাসের পরিমাণ বৃদ্ধি শুধুমাত্র তাপমাত্রা বৃদ্ধির কারণেই সম্ভব, এবং আয়তনের হ্রাস T.
এর মান হ্রাস নির্দেশ করে
মনে রাখবেন, সেলসিয়াস তাপমাত্রার বিপরীতে, পরম তাপমাত্রা ঋণাত্মক হতে পারে না।
অ্যাভোগাড্রো নীতি এবং গ্যাসের মিশ্রণ
উপরের গ্যাস আইনগুলি ছাড়াও, আদর্শ গ্যাসের জন্য রাষ্ট্রের সমীকরণটি 19 শতকের শুরুতে অ্যামেডিও অ্যাভোগাড্রো দ্বারা আবিষ্কৃত নীতির দিকে নিয়ে যায়, যা তার শেষ নাম বহন করে। এই নীতিটি প্রতিষ্ঠিত করে যে ধ্রুবক চাপ এবং তাপমাত্রায় যে কোনও গ্যাসের আয়তন সিস্টেমে পদার্থের পরিমাণ দ্বারা নির্ধারিত হয়। সংশ্লিষ্ট সূত্রটি এইরকম দেখাচ্ছে:
n/V=const যখন P, T=const।
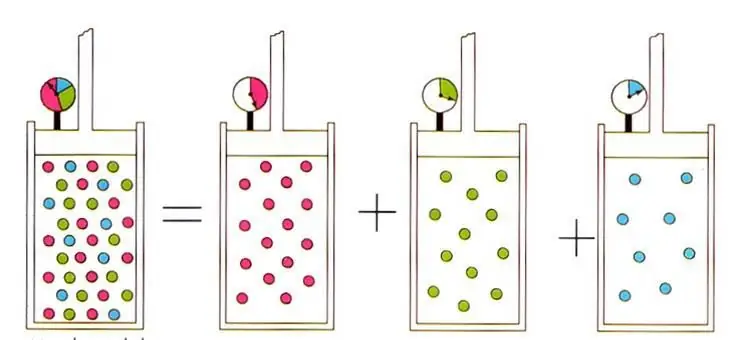
লিখিত অভিব্যক্তিটি গ্যাস মিশ্রণের জন্য আদর্শ গ্যাস পদার্থবিজ্ঞানে ডাল্টনের সুপরিচিত সূত্রের দিকে নিয়ে যায়। এইআইন বলে যে একটি মিশ্রণে গ্যাসের আংশিক চাপ তার পারমাণবিক ভগ্নাংশ দ্বারা স্বতন্ত্রভাবে নির্ধারিত হয়৷
সমস্যা সমাধানের উদাহরণ
আদর্শ গ্যাসযুক্ত অনমনীয় দেয়াল সহ একটি বন্ধ পাত্রে, গরম করার ফলে, চাপ 3 গুণ বেড়ে যায়। সিস্টেমের চূড়ান্ত তাপমাত্রা নির্ধারণ করা প্রয়োজন যদি এর প্রাথমিক মান 25 oC.
প্রথম, আসুন তাপমাত্রাকে ডিগ্রি সেলসিয়াস থেকে কেলভিনে রূপান্তর করি, আমাদের আছে:
T=25 + 273, 15=298, 15 K.
যেহেতু পাত্রের দেয়ালগুলো শক্ত, গরম করার প্রক্রিয়াটিকে আইসোকোরিক হিসেবে বিবেচনা করা যেতে পারে। এই ক্ষেত্রে, আমরা গে-লুসাক আইন প্রয়োগ করি, আমাদের আছে:
P1/T1=পি2/T 2=>
T2=P2/P1T 1.
এইভাবে, চাপের অনুপাত এবং প্রাথমিক তাপমাত্রার গুণফল থেকে চূড়ান্ত তাপমাত্রা নির্ধারণ করা হয়। ডেটাকে সমতায় প্রতিস্থাপন করে, আমরা উত্তর পাই: T2=894.45 K. এই তাপমাত্রা 621.3 oC.
এর সাথে মিলে যায়






