পদার্থবিজ্ঞানে অধ্যয়ন করার সময় মহাকাশে দেহের যান্ত্রিক গতি, তারা সর্বদা ফলস্বরূপ ত্বরণকে বিবেচনা করে। আসুন প্রবন্ধে বিবেচনা করি যে ত্বরণ কি, এবং এটি পদার্থবিজ্ঞানে কীভাবে চিহ্নিত করা হয় এবং এই মানটি গণনা করার জন্য একটি সহজ সমস্যাও সমাধান করুন।
ত্বরণ কি এবং এর প্রকারভেদ কি?
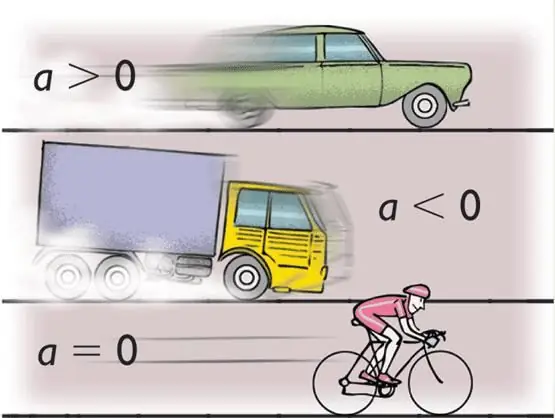
ত্বরণের অধীনে মান বোঝেন, যার অর্থ শরীরের গতিতে পরিবর্তনের গতি। গাণিতিকভাবে, এই সংজ্ঞাটি নিম্নরূপ লেখা হয়:
a=dv/dt.
যদি গতির সময় ফাংশন জানা থাকে, তবে নির্দিষ্ট সময়ে ত্বরণ গণনা করার জন্য এটির প্রথম ডেরিভেটিভ খুঁজে পাওয়া যথেষ্ট।
পদার্থবিজ্ঞানে, ত্বরণের অক্ষর হল ছোট হাতের ল্যাটিন a। যাইহোক, এটি তথাকথিত রৈখিক ত্বরণ, যা m/s2 এককে পরিমাপ করা হয়। এটি ছাড়াও, কৌণিক ত্বরণও রয়েছে। এটি কৌণিক বেগের পরিবর্তন দেখায় এবং rad/s2 এর এককে প্রকাশ করা হয়। এই ধরনের ত্বরণকে গ্রীক ছোট হাতের অক্ষর α (আলফা) দ্বারা চিহ্নিত করা হয়। মাঝে মাঝেঅক্ষর ε (এপসিলন) এটি বোঝাতে ব্যবহৃত হয়।
যদি শরীরটি একটি বাঁকা ট্র্যাজেক্টোরি বরাবর চলে, তাহলে মোট ত্বরণ দুটি অংশে বিভক্ত হয়: স্পর্শক (প্রাকৃতিক গতির পরিবর্তন নির্ণয় করে) এবং স্বাভাবিক (অভিমুখে গতির পরিবর্তন নির্ধারণ)। এই ধরনের ত্বরণ a অক্ষর দ্বারাও চিহ্নিত করা হয়, তবে সংশ্লিষ্ট সূচকগুলি ব্যবহার করে: at এবং a। স্বাভাবিককে প্রায়শই কেন্দ্রবিন্দু বলা হয় এবং স্পর্শককে প্রায়শই স্পর্শক বলা হয়।
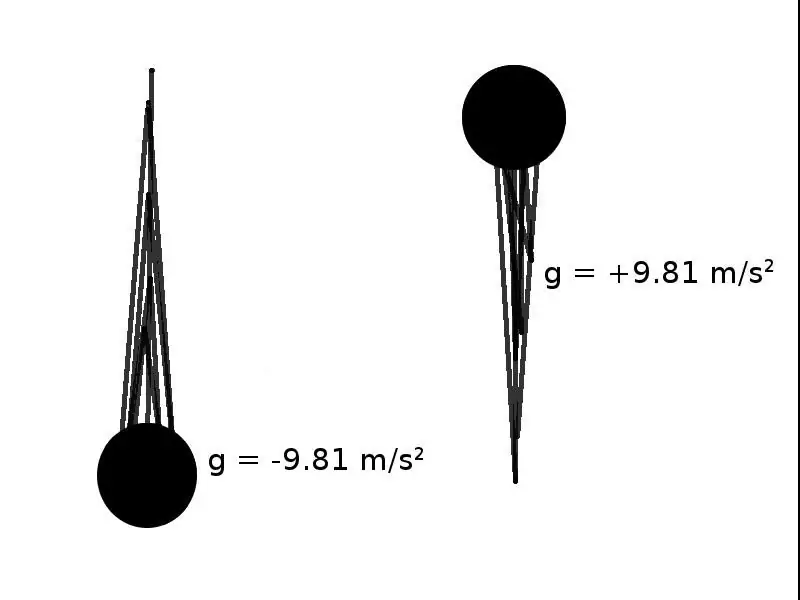
অবশেষে, গ্রহের মহাকর্ষীয় ক্ষেত্রটিতে দেহগুলি অবাধে পড়ে গেলে আরেকটি ধরণের ত্বরণ ঘটে। এটি g অক্ষর দ্বারা চিহ্নিত করা হয়।
ত্বরণের জন্য পদার্থবিজ্ঞানে সমস্যা
এটা জানা যায় যে শরীর সরল রেখায় চলে। সময়ের সাথে এর গতি নিম্নলিখিত আইন দ্বারা নির্ধারিত হয়:
v=2t2-t+4.
এটি সময় t=2.5 সেকেন্ডে শরীরের যে ত্বরণ হবে তা গণনা করা প্রয়োজন।
a এর সংজ্ঞা অনুসরণ করে আমরা পাই:
a=dv/dt=4t - 1.
অর্থাৎ, মান a রৈখিকভাবে সময়ের উপর নির্ভর করে। এটি লক্ষ্য করা কৌতূহলী যে প্রাথমিক মুহুর্তে (t=0) ত্বরণটি ছিল ঋণাত্মক, অর্থাৎ বেগ ভেক্টরের বিরুদ্ধে নির্দেশিত। এই সমীকরণে t=2.5 সেকেন্ড প্রতিস্থাপন করে আমরা সমস্যার উত্তর পাই: a=9 m/s2.






