বৈদ্যুতিক ডাইপোল। পদার্থবিদ্যা, দশম শ্রেণী। ইলেক্ট্রোডাইনামিকস

2024 লেখক: Angel Austin | [email protected]. সর্বশেষ পরিবর্তিত: 2024-01-02 17:42

10 গ্রেডে পদার্থবিদ্যা অধ্যয়ন করার সময়, ডাইপোল বিষয় বিবেচনা করা হয়। এই ধারণাটির অর্থ কী এবং এটি গণনা করার জন্য কোন সূত্র ব্যবহার করা হয়?

পরিচয়

যদি আপনি একটি অভিন্ন বৈদ্যুতিক ক্ষেত্রের স্থানে একটি ডাইপোল স্থাপন করেন, আপনি এটিকে বল রেখা হিসাবে উপস্থাপন করতে পারেন। একটি ডাইপোল এমন একটি সিস্টেম যেখানে দুটি চার্জ রয়েছে যা পরামিতিতে অভিন্ন, তবে তারা বিপরীত বিন্দু চার্জ। তদুপরি, তাদের মধ্যে দূরত্ব ডাইপোল ক্ষেত্রের যে কোনও বিন্দুর দূরত্বের চেয়ে অনেক কম হবে। ডিপোল মোমেন্টের ধারণাটি ইলেক্ট্রোডাইনামিকসের স্কুল কোর্সে অধ্যয়ন করা হয় (গ্রেড 10)।

ডাইপোলের অক্ষ একটি সরল রেখা যা উভয় চার্জের বিন্দুর মধ্য দিয়ে যায়। একটি ডাইপোল আর্ম হল একটি ভেক্টর যা একটি চার্জকে সংযুক্ত করে এবং একই সময়ে ঋণাত্মক চার্জযুক্ত কণা থেকে ধনাত্মক চার্জযুক্ত কণাগুলিতে যায়। একটি বৈদ্যুতিক ডাইপোল একটি ডাইপোল বা বৈদ্যুতিক মুহুর্তের মতো অবস্থার উপস্থিতি দ্বারা চিহ্নিত করা হয়।

সংজ্ঞা অনুসারে, একটি ডাইপোল মোমেন্ট হল একটি ভেক্টর যা সংখ্যাগতভাবে ডাইপোল চার্জ এবং এর বাহুর গুণফলের সমান। তদুপরি, এটি ডাইপোলের কাঁধের সাথে সহ-নির্দেশিত হয়। শক্তির যোগফলের শূন্য সমতায়, আমরা মুহূর্তের মান গণনা করি। ডাইপোল মোমেন্ট এবং এর মধ্যে বিদ্যমান কোণের জন্যবৈদ্যুতিক ক্ষেত্রের দিকনির্দেশনা, একটি যান্ত্রিক মুহূর্তের উপস্থিতি বৈশিষ্ট্যযুক্ত।

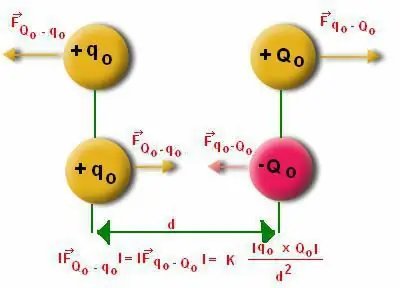
প্রায়শই মানুষ ডাইপোল কাঠামোর উপর কাজ করে এমন মডুলাস গণনা করা কঠিন বলে মনে করেন। এখানে কোণ "আলফা" গণনা করার অদ্ভুততা বিবেচনা করা প্রয়োজন। এটি জানা যায় যে ডাইপোল ভারসাম্যপূর্ণ অবস্থান থেকে বিচ্যুত হয়। কিন্তু ডাইপোল মুহূর্তটির নিজেই একটি পুনরুদ্ধারকারী চরিত্র রয়েছে, কারণ এটি গতিশীল থাকে।

গণনা

যখন এই ডাইপোল মুহূর্তটিকে একটি অসংলগ্ন বৈদ্যুতিক ক্ষেত্রের মাধ্যমে স্থাপন করা হয়, তখন অনিবার্যভাবে একটি শক্তির উদ্ভব হয়। এই ধরনের পরিবেশে, বাহিনীর যোগফলের সূচক শূন্য হবে না। ফলস্বরূপ, একটি বিন্দু অক্ষর সহ ডাইপোল মুহূর্তটিতে বাহিনী কাজ করে। ডাইপোল বাহুর আকার অনেক ছোট।

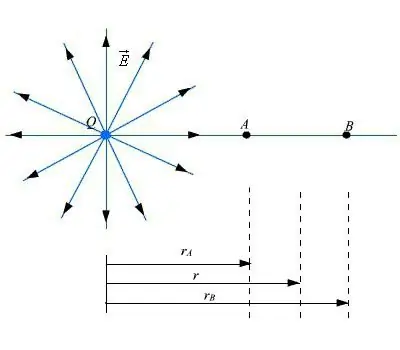
সূত্রটি এভাবে লেখা যেতে পারে: F=q (E2 - E1)=qdE, যেখানে d হল বৈদ্যুতিক ক্ষেত্রের পার্থক্য।

অধ্যয়নের অধীনে শারীরিক ধারণার বৈশিষ্ট্যগুলি অনুসন্ধান করুন

আসুন বিষয়টিকে আরও দেখুন। বৈদ্যুতিক ক্ষেত্রের বৈশিষ্ট্য কী তা নির্ধারণ করার জন্য, যদি এটি চার্জের একটি সিস্টেম ব্যবহার করে তৈরি করা হয় এবং একটি ছোট জায়গায় স্থানীয়করণ করা হয়, তবে বেশ কয়েকটি গণনা করা প্রয়োজন। একটি উদাহরণ পরমাণু এবং অণু দ্বারা উপস্থাপন করা হয়েছে, যেগুলির গঠনে বৈদ্যুতিকভাবে চার্জযুক্ত নিউক্লিয়াস এবং ইলেকট্রন রয়েছে৷

যদি কণাগুলি যেখানে অবস্থিত সেই ক্ষেত্রটি তৈরি করে এমন মাত্রার চেয়ে বেশি দূরত্বে একটি ক্ষেত্র অনুসন্ধান করার প্রয়োজন হয় তবে আমরা অনেকগুলি সঠিক সূত্র ব্যবহার করব যা অত্যন্ত জটিল। এটা সহজ ব্যবহার করা সম্ভবআনুমানিক অভিব্যক্তি। আসুন আমরা ধরে নিই যে চার্জের বিন্দু সেট q_{k বৈদ্যুতিক ক্ষেত্র তৈরিতে অংশ নেয়। তারা একটি ছোট জায়গায় অবস্থিত।}

ক্ষেত্রটির বৈশিষ্ট্যের গণনা করতে, এটিকে সিস্টেমের সমস্ত চার্জ একত্রিত করার অনুমতি দেওয়া হয়। এই ধরনের সিস্টেমকে বিন্দু চার্জ হিসাবে বিবেচনা করা হয় Q. মাত্রার সূচকগুলি মূল সিস্টেমে থাকা চার্জগুলির সমষ্টি হবে৷

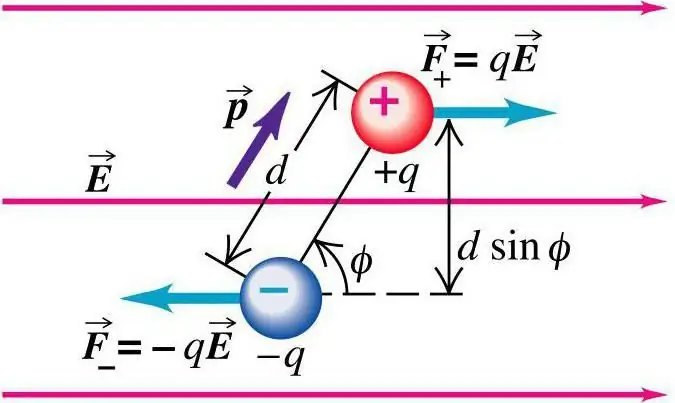
চার্জের অবস্থান

আসুন কল্পনা করা যাক যে চার্জের অবস্থানটি যে কোনো স্থানে নির্দেশিত হয়েছে যেখানে চার্জ সিস্টেম q_{k অবস্থিত। অবস্থানে পরিবর্তন করার সময়, যদি এটি একটি ছোট এলাকায় সীমাবদ্ধ থাকে, তাহলে এই ধরনের প্রভাব হবে নগণ্য, দৃষ্টিকোণে ক্ষেত্রের কাছে প্রায় অদৃশ্য। বৈদ্যুতিক ক্ষেত্রের শক্তি এবং সম্ভাবনার আনুমানিক সীমার মধ্যে, প্রথাগত সূত্র ব্যবহার করে নির্ধারণ করা হয়৷}

যখন সিস্টেমের মোট চার্জের যোগফল শূন্য হয়, তখন নির্দেশিত আনুমানিকতার পরামিতিগুলি মোটামুটি দেখাবে। এটি এই উপসংহারে আসার কারণ দেয় যে বৈদ্যুতিক ক্ষেত্রটি কেবল অনুপস্থিত। যদি আরও সঠিক আনুমানিক প্রাপ্তির প্রয়োজন হয়, মানসিকভাবে সিস্টেমের ইতিবাচক এবং নেতিবাচক চার্জগুলির পৃথক গ্রুপ সংগ্রহ করুন যা বিবেচনা করা হচ্ছে৷

অন্যদের তুলনায় তাদের "কেন্দ্রের" স্থানচ্যুতির ক্ষেত্রে, এই ধরনের সিস্টেমের ক্ষেত্রের পরামিতিগুলিকে এমন একটি ক্ষেত্র হিসাবে বর্ণনা করা যেতে পারে যেখানে দুটি বিন্দু চার্জ রয়েছে, মাত্রায় সমান এবং চিহ্নে বিপরীত। এটি উল্লেখ্য যে তারা অন্যদের সাথে বাস্তুচ্যুত হয়। সরবরাহ করতেএই আনুমানিকতার পরামিতিগুলির পরিপ্রেক্ষিতে চার্জ সিস্টেমের আরও সঠিক বৈশিষ্ট্যের জন্য, একটি বৈদ্যুতিক ক্ষেত্রের একটি ডাইপোলের বৈশিষ্ট্যগুলি অধ্যয়ন করা প্রয়োজন৷

শব্দটির ভূমিকা

আসুন সংজ্ঞায় ফিরে আসা যাক। একটি বৈদ্যুতিক ডাইপোল হল একটি সিস্টেমের সংজ্ঞা যার দুটি পয়েন্ট চার্জ রয়েছে। তাদের একই আকার এবং বিপরীত চিহ্ন রয়েছে। তদুপরি, এই জাতীয় চিহ্নগুলি অন্যান্য চিহ্নগুলির তুলনায় ছোট দূরত্বে অবস্থিত৷

আপনি একটি ডাইপোল দ্বারা তৈরি প্রক্রিয়াটির বৈশিষ্ট্য গণনা করতে পারেন, এবং এটি দুটি বিন্দু চার্জ দ্বারা প্রতিনিধিত্ব করা হয়: +q এবং −q, এবং তারা অন্যদের তুলনায় একটি দূরত্বে অবস্থিত।

গণনার ক্রম

আসুন শুরু করা যাক ডাইপোলের অক্ষীয় পৃষ্ঠে থাকা সম্ভাব্যতা এবং তীব্রতা গণনা করে। এটি একটি সরল রেখা যা দুটি চার্জের মধ্যে চলে। তবে শর্ত থাকে যে বিন্দু A এমন দূরত্বে অবস্থিত যা ডাইপোলের কেন্দ্রীয় অংশের সাথে r আপেক্ষিক, এবং যদি এটি r >> a হয়, এই বিন্দুতে ক্ষেত্রের সম্ভাব্যতার জন্য সুপারপজিশনের নীতি অনুসারে, এটি যুক্তিসঙ্গত হবে বৈদ্যুতিক ডাইপোলের পরামিতি গণনা করতে অভিব্যক্তিটি ব্যবহার করুন।

শক্তি ভেক্টরের মাত্রা সুপারপজিশনের নীতি দ্বারা গণনা করা হয়।ক্ষেত্রের শক্তি গণনা করতে, সম্ভাব্য এবং ক্ষেত্রের শক্তির অনুপাতের ধারণাটি ব্যবহার করা হয়:

E_{x=−Δφ /Δx.}

এই ধরনের পরিস্থিতিতে, তীব্রতা ভেক্টরের দিকটি দ্বিমেরু অক্ষের সাপেক্ষে অনুদৈর্ঘ্যভাবে নির্দেশিত হয়। এর মডুলাস গণনা করতে, আদর্শ সূত্রটি প্রযোজ্য।

গুরুত্বপূর্ণস্পষ্টীকরণ

এটি বিবেচনায় নেওয়া উচিত যে বৈদ্যুতিক ডাইপোল ক্ষেত্রের দুর্বলতা একটি বিন্দু চার্জের অভিজ্ঞতার চেয়ে দ্রুত ঘটে। ডাইপোল ক্ষেত্রের সম্ভাবনার ক্ষয় দূরত্বের বর্গক্ষেত্রের বিপরীতভাবে সমানুপাতিক, এবং ক্ষেত্রের শক্তি দূরত্বের ঘনক্ষেত্রের বিপরীতভাবে সমানুপাতিক।

অনুরূপ, কিন্তু আরও কষ্টকর পদ্ধতি ব্যবহার করে, ডাইপোলের সম্ভাব্য এবং ক্ষেত্রের শক্তির পরামিতিগুলি নির্বিচারে পাওয়া যায়, যার অবস্থানের পরামিতিগুলি মেরু স্থানাঙ্কের মতো একটি গণনা পদ্ধতি ব্যবহার করে নির্ধারিত হয়: দূরত্ব বৈদ্যুতিক ডাইপোলের কেন্দ্র (r) এবং কোণ (θ)।

টেনশন ভেক্টর ব্যবহার করে গণনা

তীব্রতা ভেক্টর E এর ধারণাটি দুটি বিন্দুতে বিভক্ত:

• রেডিয়াল (E_{r), যা সরলরেখার সাপেক্ষে অনুদৈর্ঘ্য দিকে পরিচালিত হয়।}
• এই ধরনের একটি সরল রেখা নির্দিষ্ট বিন্দু এবং ডাইপোলের কেন্দ্রকে এর সাথে লম্বের সাথে সংযুক্ত করে E_θ।

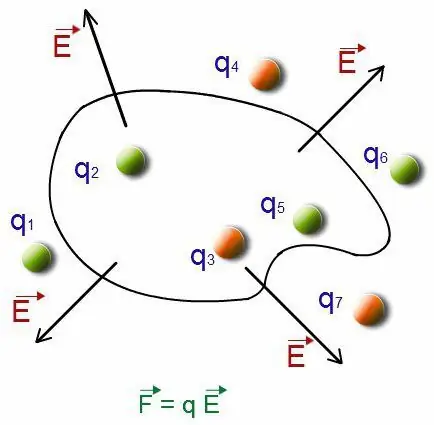
প্রতিটি উপাদানের এই পচনটি পরিলক্ষিত বিন্দুর সমস্ত স্থানাঙ্কের সাথে ঘটে যাওয়া পরিবর্তনের সময় নির্দেশিত হয়। সম্ভাব্য পরিবর্তনের সাথে ক্ষেত্রের শক্তি সূচকের সাথে সম্পর্কিত অনুপাত দ্বারা আপনি এটি খুঁজে পেতে পারেন৷

ক্ষেত্রের শক্তিতে ভেক্টর উপাদান খুঁজে বের করা, ভেক্টরের দিক থেকে পর্যবেক্ষণ বিন্দুর স্থানচ্যুতির কারণে সম্ভাব্য পরিবর্তনগুলির মধ্যে সম্পর্কের প্রকৃতি স্থাপন করা গুরুত্বপূর্ণ।

লম্ব উপাদান গণনা করুন

হয়ে গেলেএই পদ্ধতির জন্য, এটি বিবেচনা করা গুরুত্বপূর্ণ যে একটি ছোট লম্ব স্থানচ্যুতিতে মাত্রার জন্য অভিব্যক্তিটি কোণ পরিবর্তন করে নির্ধারণ করা হবে: Δl=rΔθ.এই ক্ষেত্রের উপাদানটির মাত্রার পরামিতিগুলি সমান হবে৷

অনুপাত প্রাপ্ত করার পরে, এই ক্ষেত্রের বল রেখার সাথে একটি ছবি তৈরি করার জন্য একটি নির্বিচারে বৈদ্যুতিক ডাইপোলের ক্ষেত্র নির্ধারণ করা সম্ভব।

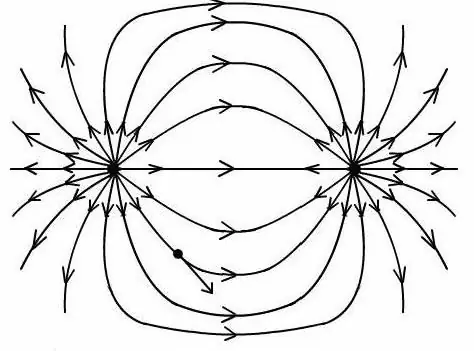
এটি বিবেচনা করা গুরুত্বপূর্ণ যে একটি ডাইপোলের সম্ভাব্যতা এবং ক্ষেত্রের শক্তি নির্ধারণের জন্য সমস্ত সূত্রগুলি শুধুমাত্র একটি ডাইপোল চার্জের মান এবং তাদের মধ্যে দূরত্বের গুণফলের উপর কাজ করে৷

ডিপোল মোমেন্ট

বর্ণিত কাজের শিরোনামটি বৈদ্যুতিক ধরণের বৈশিষ্ট্যগুলির একটি সম্পূর্ণ বিবরণ। এটির নাম "ডিপোল মোমেন্ট অফ সিস্টেম"।

একটি ডাইপোলের সংজ্ঞা অনুসারে, যা বিন্দু চার্জের একটি সিস্টেম, এটি খুঁজে পাওয়া যায় যে এটি অক্ষীয় প্রতিসাম্যের উপস্থিতি দ্বারা চিহ্নিত করা হয়, যখন অক্ষ একটি সরল রেখা হয় যা বিভিন্ন চার্জের মধ্য দিয়ে যায়।

ডাইপোলের সম্পূর্ণ বৈশিষ্ট্য সেট করতে, অক্ষের দিকনির্দেশনা নির্দেশ করুন। গণনার সরলতার জন্য, ডাইপোল মোমেন্ট ভেক্টর নির্দিষ্ট করা যেতে পারে। এর মাত্রার মান ডাইপোল মোমেন্টের মাত্রার সমান, এবং দিক ভেক্টর এটির কাকতালীয় এবং ডাইপোলের অক্ষের দ্বারা পৃথক হয়। সুতরাং, p=qa যদি a ভেক্টরের দিক হয় যা ডাইপোলের ঋণাত্মক এবং ধনাত্মক চার্জকে সংযুক্ত করে।

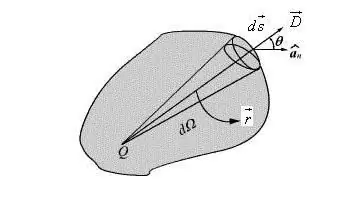
ডাইপোলের এই জাতীয় বৈশিষ্ট্যের ব্যবহার সুবিধাজনক এবং বেশিরভাগ ক্ষেত্রে সূত্রটিকে সরল করা এবং এটিকে রূপ দেওয়া সম্ভব করে তোলে।ভেক্টর নির্বিচারে দিকনির্দেশের একটি বিন্দুতে ডাইপোল ক্ষেত্রের সম্ভাব্যতার বর্ণনা একটি ভেক্টর আকারে লেখা হয়।

একটি ডাইপোলের ভেক্টর বৈশিষ্ট্য এবং এর ডাইপোল মোমেন্টের মতো ধারণাগুলির প্রবর্তন একটি সরলীকৃত মডেল ব্যবহার করে সঞ্চালিত হতে পারে - একটি অভিন্ন ক্ষেত্রের একটি বিন্দু চার্জ, যার মধ্যে চার্জের একটি সিস্টেম রয়েছে, যার জ্যামিতিক মাত্রাগুলি বিবেচনায় নিতে হবে না, তবে ডাইপোল মুহূর্তটি জানা গুরুত্বপূর্ণ। এটি গণনা সম্পাদনের জন্য একটি পূর্বশর্ত।

একটি ডাইপোল কেমন আচরণ করে

এমন পরিস্থিতির উদাহরণে ডাইপোলের আচরণ দেখা যায়। দুটি বিন্দু চার্জের অবস্থান একে অপরের সাপেক্ষে দূরত্বের একটি নির্দিষ্ট চরিত্র রয়েছে। এগুলিকে একটি অভিন্ন বৈদ্যুতিক ক্ষেত্রের একটি ডাইপোলের অবস্থায় স্থাপন করা হয়েছিল। প্রক্রিয়ার উপর পর্যবেক্ষণ করেছেন। পদার্থবিদ্যার পাঠে (ইলেক্ট্রোডায়নামিক্স), এই ধারণাটি বিশদভাবে বিবেচনা করা হয়। ক্ষেত্র থেকে চার্জ পর্যন্ত, বাহিনীর ক্রিয়া সঞ্চালিত হয়:

F=±qE

এরা মাত্রায় সমান এবং দিক বিপরীত। ডাইপোলের উপর কাজ করে এমন মোট শক্তির সূচক শূন্য। যেহেতু এই ধরনের শক্তি বিভিন্ন বিন্দুতে প্রভাব ফেলে, মোট মুহূর্ত হবে:

M=Fa sin a=qEa sin a=pE sin a

α হল ক্ষেত্র শক্তি ভেক্টর এবং ডাইপোল মোমেন্ট ভেক্টরের সাথে সংযোগকারী কোণ। একটি বল মোমেন্টের উপস্থিতির কারণে, সিস্টেমের ডাইপোল মোমেন্ট বৈদ্যুতিক ক্ষেত্রের শক্তি ভেক্টরের দিকে ফিরে যেতে থাকে।

বৈদ্যুতিক ডাইপোল একটি ধারণা যা পরিষ্কারভাবে বোঝা গুরুত্বপূর্ণ। আপনি ইন্টারনেটে এটি সম্পর্কে আরও পড়তে পারেন। এছাড়াও এটা পারে10 শ্রেণীতে স্কুলে পদার্থবিদ্যা পাঠে অধ্যয়ন করতে, যেমনটি আমরা উপরে বলেছি।