একটি রৈখিক ফাংশন একটি পৃষ্ঠ বরাবর আঁকা একটি সরল রেখা। এটা বিভিন্ন ধরনের এবং মডেল বিভক্ত করা যেতে পারে। নীচে আমরা এটি পাওয়ার জন্য সূত্রগুলি বিবেচনা করব, পাশাপাশি সমতলে এর পরিপূর্ণতা অর্জন করব। অঙ্কনগুলিতে, আপনি এটি সম্পূর্ণরূপে যাচাই করতে পারেন এবং এটি দেখতে কেমন হওয়া উচিত তা বুঝতে পারেন৷
লিনিয়ার ফাংশন y=kx + b
এই মানটি একটি ভিউতে একটি পরিবর্তনশীলের সঠিক পরিমাপ। বৃদ্ধি একটি রৈখিক ফাংশনের মৌলিক বৈশিষ্ট্য বোঝায়, এটি বর্ধিত আর্গুমেন্টের সমানুপাতিক হয়ে যায়। অন্য কথায়, ফাংশনটি সরাসরি আনুপাতিকতার একটি সাধারণীকরণের প্রতিনিধিত্ব করে। একটি সরল রেখা একটি রৈখিক ফাংশনের একটি গ্রাফ। এখান থেকে এর নাম এসেছে। একটি বাস্তব পরিবর্তনশীল আরেকটি বাস্তব ফাংশন স্পর্শ করে।
বৈশিষ্ট্য
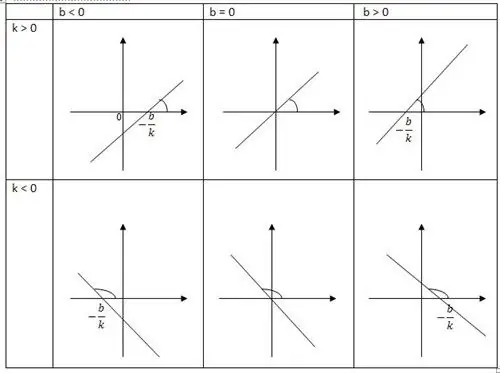
রৈখিক ফাংশন হল একটি সরলরেখার একটি জেনাট্রিক্স, যার x-অক্ষের একটি ধনাত্মক দিক রয়েছে। এর একটি সংজ্ঞায়িত ঢাল ফ্যাক্টর হল k, এটি a কোণের স্পর্শক নির্ধারণ করে। x-অক্ষের ধনাত্মক দিকে গঠিত সরলরেখাটি হল k। অন্য স্থানাঙ্ক b নির্দেশ করেবিন্দু স্থানাঙ্ক, সেইসাথে অক্ষের সাথে লাইনের ছেদ।
নন-লিনিয়ার ফাংশন কি?
যেসব ফাংশন রৈখিক নয় তাকে নন-লিনিয়ার বলে। এটি ভেরিয়েবলের মধ্যে একটি গাণিতিক সম্পর্ক। অরৈখিককে y=ax + b হিসাবে প্রকাশ করা যায় না। এই শব্দটি সেই মুহুর্তগুলিতে ব্যবহৃত হয় যখন সাধারণ ক্ষেত্রে অধ্যয়ন করা প্রয়োজন। এই প্রক্রিয়াটি নিম্ন ডিগ্রী দিয়ে শুরু হয়। এই ক্ষেত্রে, দ্বিঘাত সংশোধন বিবেচনা করা হয়। এই ধরনের ফাংশন ক্রমাগত বক্রতা আছে.
বিবেচিত অ-রৈখিক সমীকরণটি নির্বিচারে। একটি নন-লিনিয়ার ফাংশনের উদাহরণ হল y=x2। "রৈখিক ফাংশন" শব্দটি প্রায়শই ব্যবহার করা হয়, একটি পরিমার্জন এবং "সমজাতীয়" যোগ করে। এটি X এর একটি সঠিক রৈখিক ম্যাপিংয়ে প্রয়োগ করা যেতে পারে, যা একটি ভেক্টর স্থান। একটি রৈখিক ফাংশন পুরো সিস্টেমের মতো।






