Titias-Bode নিয়ম (কখনও কখনও কেবল বোডের আইন বলা হয়) হল অনুমান যে সূর্য সহ কিছু অরবিটাল সিস্টেমে দেহগুলি গ্রহের ক্রম অনুসারে আধা-অক্ষ বরাবর ঘোরে। সূত্রটি পরামর্শ দেয় যে, বাইরের দিকে প্রসারিত হলে, প্রতিটি গ্রহ সূর্য থেকে আগেরটির চেয়ে প্রায় দ্বিগুণ দূরে থাকবে৷
অনুমানটি সঠিকভাবে সেরেস (গ্রহাণু বেল্টে) এবং ইউরেনাসের কক্ষপথের ভবিষ্যদ্বাণী করেছিল, কিন্তু নেপচুনের কক্ষপথ নির্ধারণ করতে ব্যর্থ হয়েছিল এবং অবশেষে সৌরজগতের গঠন তত্ত্ব দ্বারা প্রতিস্থাপিত হয়েছিল। এটির নামকরণ করা হয়েছে জোহান ড্যানিয়েল টিটিয়াস এবং জোহান এলার্ট বোডের নামে।

উৎপত্তি
1715 সালে প্রকাশিত ডেভিড গ্রেগরির এলিমেন্টস অফ অ্যাস্ট্রোনমিতে বোডের সূত্রের আনুমানিক একটি সিরিজের প্রথম উল্লেখ পাওয়া যায়। এতে তিনি বলেছেন: “… ধরে নিচ্ছি যে সূর্য থেকে পৃথিবীর দূরত্ব দশটি সমান ভাগে বিভক্ত, যার মধ্যে বুধের দূরত্ব হবে প্রায় চারটি, শুক্র থেকে সাতটি, মঙ্গল গ্রহ থেকে পনেরোটি, বৃহস্পতি বায়ান্ন ভাগ থেকে।, এবং শনি পঁচানব্বই থেকে1724 সালে ক্রিশ্চিয়ান উলফের প্রকাশিত একটি রচনায় অনুরূপ একটি পরামর্শ, সম্ভবত গ্রেগরির দ্বারা অনুপ্রাণিত হয়।
1764 সালে, চার্লস বননেট তার প্রকৃতির মনন বইয়ে বলেছিলেন: "আমরা আমাদের সৌরজগত [অর্থাৎ প্রধান গ্রহ এবং তাদের উপগ্রহ] তৈরি করে এমন সতেরোটি গ্রহ জানি, কিন্তু আমরা নিশ্চিত নই যে তারা আর নেই।" এর জন্য, বনেটের রচনার 1766 সালের অনুবাদে, জোহান ড্যানিয়েল টিটিয়াস পৃষ্ঠা 7 এর নীচে এবং 8 পৃষ্ঠার শীর্ষে তার নিজের দুটি অনুচ্ছেদ যুক্ত করেছেন। নতুন ইন্টারপোলেটেড অনুচ্ছেদটি বননেটের মূল পাঠে পাওয়া যায় না: ইতালীয় ভাষায়ও নয়। বা কাজের ইংরেজি অনুবাদও নয়।
টাইটিয়াসের আবিষ্কার
টাইটিয়াসের আন্তঃকালিত পাঠে দুটি অংশ রয়েছে। প্রথমটি সূর্য থেকে গ্রহের দূরত্বের ক্রম ব্যাখ্যা করে। এতে সূর্য থেকে বৃহস্পতি গ্রহের দূরত্ব সম্পর্কেও কিছু শব্দ রয়েছে। কিন্তু এখানেই লেখার শেষ নয়।
Titius-Bode নিয়মের সূত্র সম্পর্কে কয়েকটি শব্দ বলা মূল্যবান। গ্রহগুলির মধ্যে দূরত্বের দিকে মনোযোগ দিন এবং খুঁজে বের করুন যে তাদের প্রায় সবগুলিই তাদের শারীরিক আকারের অনুপাতে একে অপরের থেকে আলাদা। সূর্য থেকে শনির দূরত্বকে 100 ভাগে ভাগ করুন; তারপরে বুধ সূর্য থেকে চারটি অংশ দ্বারা পৃথক হয়; শুক্র - 4 + 3=7 যেমন অংশে; পৃথিবী - 4+6=10 দ্বারা; মঙ্গল - 4+12=16 দ্বারা।
কিন্তু মনে রাখবেন যে মঙ্গল থেকে বৃহস্পতি পর্যন্ত এই সুনির্দিষ্ট অগ্রগতি থেকে একটি বিচ্যুতি রয়েছে। 4+24=28 এর একটি স্থান মঙ্গল গ্রহ থেকে অনুসরণ করে, কিন্তু এখনও পর্যন্ত সেখানে একটি গ্রহ আবিষ্কৃত হয়নি। কিন্তু লর্ড আর্কিটেক্টের কি এই জায়গাটা খালি রাখা উচিত? কখনই না। তাইআসুন ধরে নিই যে এই স্থানটি নিঃসন্দেহে মঙ্গলের এখনও অনাবিষ্কৃত চাঁদের অন্তর্গত, এবং যোগ করুন যে সম্ভবত বৃহস্পতির চারপাশে এখনও কয়েকটি ছোট চাঁদ রয়েছে যেগুলি এখনও কোনও টেলিস্কোপ দ্বারা দেখা যায়নি৷

আশাকের উত্থান
1772 সালে, জোহান এলার্ট বোডে, পঁচিশ বছর বয়সে, তার জ্যোতির্বিদ্যা সংকলন Anleitung zur Kenntniss des gestirnten Himmels ("নক্ষত্রযুক্ত আকাশের জ্ঞানের নির্দেশিকা") এর দ্বিতীয় সংস্করণটি সম্পূর্ণ করেন, যেখানে তিনি নিম্নলিখিত পাদটীকা যোগ করা হয়েছে, মূলত আনসোর্স, কিন্তু পরবর্তী সংস্করণগুলিতে উল্লেখ করা হয়েছে। বোডের স্মৃতিকথায় একজন তার কর্তৃত্বের সুস্পষ্ট স্বীকৃতি সহ তিতিয়াসের একটি উল্লেখ খুঁজে পেতে পারেন।

মতামত নির্দেশ
এইভাবে শেষোক্ত ধ্বনির উপস্থাপনায় টাইটিয়াস-বোডের নিয়ম: যদি সূর্য থেকে শনির দূরত্ব 100 এর সমান ধরা হয়, তবে বুধ সূর্য থেকে চারটি অংশ দ্বারা পৃথক হয়। শুক্র - 4+3=7। পৃথিবী - 4+6=10। মঙ্গল - 4+12=16.
এখন এই আদেশকৃত অগ্রগতিতে একটি ফাঁক রয়েছে। মঙ্গল গ্রহের পরে 4+24=28 গণনা সহ একটি স্থান অনুসরণ করে, যেখানে এখনও একটি গ্রহ দেখা যায়নি। আমরা কি বিশ্বাস করতে পারি যে মহাবিশ্বের প্রতিষ্ঠাতা এই স্থানটি খালি রেখেছিলেন? অবশ্যই না. এখান থেকে আমরা গণনার আকারে বৃহস্পতির দূরত্বে আসি 4+48=52 এবং অবশেষে, শনির দূরত্ব - 4+96=100।

সমস্ত নির্দিষ্ট টাইপোলজি এবং অরবিটাল রেডিআই সম্পর্কিত এই দুটি বিবৃতি প্রাচীন থেকে এসেছে বলে মনে হচ্ছেজ্যোতির্বিদ্যা এই তত্ত্বগুলির মধ্যে অনেকগুলি সপ্তদশ শতাব্দীর আগের।
প্রভাব
টাইটিয়াস ছিলেন জার্মান দার্শনিক ক্রিশ্চিয়ান ফ্রেইহর ফন উলফের (1679-1754) ছাত্র। বননেটের রচনায় সন্নিবেশিত পাঠ্যের দ্বিতীয় অংশটি ভন উলফের 1723 সালের কাজের উপর ভিত্তি করে তৈরি করা হয়েছে, Vernünftige Gedanken von den Wirkungen der Natur.
বিংশ শতাব্দীর সাহিত্য একজন জার্মান দার্শনিককে টাইটিয়াস-বোড শাসনের লেখকত্ব প্রদান করে। যদি তাই হয়, তিতিয়াস তার কাছ থেকে শিখতে পারে। আরেকটি পুরানো রেফারেন্স জেমস গ্রেগরি 1702 সালে তার Astronomiae Physicae et geometryae Elementa-তে লিখেছিলেন, যেখানে গ্রহের দূরত্বের ক্রম 4, 7, 10, 16, 52 এবং 100 অনুপাতের জ্যামিতিক অগ্রগতিতে পরিণত হয়েছিল।
এটি নিউটনের সবচেয়ে কাছের সূত্র, এবং জার্মানিতে বনেটের বই প্রকাশিত হওয়ার কয়েক বছর আগে বেঞ্জামিন মার্টিন এবং টমাস সিয়ার্ডের লেখাতেও এটি পাওয়া গেছে।
আরও কাজ এবং ব্যবহারিক প্রভাব
Titius এবং Bode আশা করেছিলেন যে আইনটি নতুন গ্রহের আবিষ্কারের দিকে পরিচালিত করবে এবং প্রকৃতপক্ষে, ইউরেনাস এবং সেরেসের আবিষ্কার, যার মধ্যে দূরত্বটি আইনের সাথে ভালভাবে একমত, বৈজ্ঞানিক বিশ্বের দ্বারা এর গ্রহণযোগ্যতায় অবদান রেখেছে।
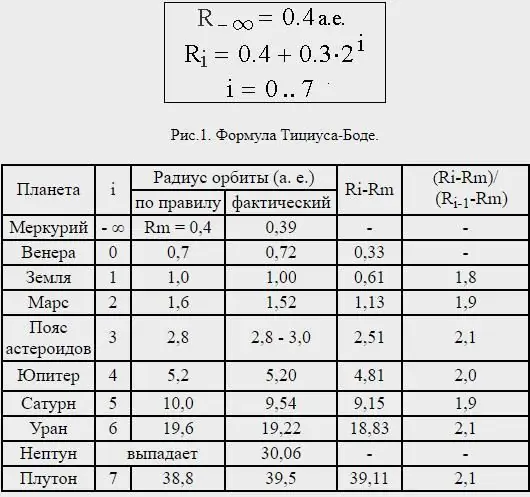
তবে, নেপচুনের দূরত্ব খুবই অসামঞ্জস্যপূর্ণ ছিল, এবং প্রকৃতপক্ষে প্লুটো - এখন একটি গ্রহ হিসাবে বিবেচিত নয় - একটি গড় দূরত্বে রয়েছে যা ইউরেনাসের বাইরের পরবর্তী গ্রহের জন্য ভবিষ্যদ্বাণী করা টিটিয়াস-বোড আইনের সাথে প্রায় মিলে যায়৷
আদি প্রকাশিত আইনটি সমস্ত পরিচিত গ্রহ - বুধ এবং শনি - এর মধ্যে একটি ব্যবধান সহ প্রায় সন্তুষ্ট ছিলচতুর্থ এবং পঞ্চম গ্রহ। 1781 সালে ইউরেনাস আবিষ্কারের আগ পর্যন্ত এটিকে একটি আকর্ষণীয়, কিন্তু খুব বেশি গুরুত্ব দেওয়া হয়নি, যা এই সিরিজের সাথে খাপ খায়।
এই আবিষ্কারের উপর ভিত্তি করে, বোডে একটি পঞ্চম গ্রহের সন্ধানের আহ্বান জানিয়েছে। সেরেস, গ্রহাণু বেল্টের বৃহত্তম বস্তু, 1801 সালে বোডের পূর্বাভাসিত অবস্থানে পাওয়া গিয়েছিল। 1846 সালে নেপচুন আবিষ্কৃত না হওয়া পর্যন্ত বোডের আইন ব্যাপকভাবে গৃহীত হয়েছিল এবং আইনের সাথে অসামঞ্জস্যপূর্ণ দেখানো হয়েছিল।
একই সময়ে, বেল্টে আবিষ্কৃত বিপুল সংখ্যক গ্রহাণু গ্রহের তালিকা থেকে সেরেসকে অতিক্রম করেছে। বোডের আইনটি 1898 সালে জ্যোতির্বিজ্ঞানী এবং যুক্তিবিদ চার্লস স্যান্ডার্স পিয়ার্স ভুল যুক্তির উদাহরণ হিসাবে আলোচনা করেছিলেন।

সমস্যার বিকাশ
1930 সালে প্লুটোর আবিষ্কার সমস্যাটিকে আরও জটিল করে তোলে। যদিও এটি বোডের আইন দ্বারা ভবিষ্যদ্বাণী করা অবস্থানের সাথে মেলেনি, তবে এটি নেপচুনের জন্য আইনের ভবিষ্যদ্বাণী করা অবস্থান সম্পর্কে ছিল। যাইহোক, পরবর্তীকালে কুইপার বেল্টের আবিষ্কার, এবং বিশেষ করে এরিস বস্তু, যেটি প্লুটোর চেয়েও বেশি বিশাল কিন্তু বোডের নিয়ম মেনে চলে না, সূত্রটিকে আরও অসম্মানিত করেছে।
সেরদার অবদান
The Jesuit Thomas Cerda 1760 সালে বার্সেলোনায় বিখ্যাত জ্যোতির্বিজ্ঞানের কোর্স দেন কলেজ অফ সান্ট জাউমে ডি কর্ডেলে (কর্ডেলের রাজকীয় ও রাজকীয় সেমিনারী) কলেজের গণিতের রাজকীয় চেয়ারে। Cerdas' Tratado-এ, গ্রহের দূরত্ব দেখা যায়, কেপলারের তৃতীয় সূত্র প্রয়োগ করে 10-3 এর নির্ভুলতা সহ প্রাপ্ত হয়।
যদি আমরা পৃথিবী থেকে দূরত্ব 10 হিসাবে নিই এবংপূর্ণসংখ্যা পর্যন্ত বৃত্তাকার, জ্যামিতিক অগ্রগতি [(Dn x 10) - 4] / [(Dn-1 x 10) - 4]=2, n=2 থেকে n=8 পর্যন্ত, প্রকাশ করা যেতে পারে। এবং কেপলারের অসঙ্গতিতে একটি বৃত্তাকার অভিন্ন কাল্পনিক গতি ব্যবহার করে, প্রতিটি গ্রহের অনুপাতের সাথে সম্পর্কিত Rn মানগুলি rn=(Rn - R1) / (Rn-1 - R1) হিসাবে পাওয়া যেতে পারে, যার ফলে 1.82 হয়; 1, 84; 1, 86; 1.88 এবং 1.90, যেখানে rn=2 - 0.02 (12 - n) কেপলারিয়ান ধারাবাহিকতা এবং টিটিয়াস-বোড আইনের মধ্যে একটি সুস্পষ্ট সম্পর্ক, যা একটি এলোমেলো সংখ্যাগত কাকতালীয় হিসাবে বিবেচিত হয়। গণনার ফলাফল দুটির কাছাকাছি, তবে ডিউসটিকে 1, 82 নম্বরের একটি রাউন্ডিং হিসাবে বিবেচনা করা যেতে পারে।

n=1 থেকে n=8 পর্যন্ত গ্রহটির গড় গতি সূর্য থেকে দূরত্ব কমায় এবং n=7 (অরবিটাল রেজোন্যান্স) থেকে পুনরুদ্ধার করতে n=2-এ অভিন্ন পতন থেকে আলাদা। এটি সূর্য থেকে বৃহস্পতির দূরত্বকে প্রভাবিত করে। যাইহোক, নিবন্ধটি যে কুখ্যাত নিয়মের কাঠামোর মধ্যে অন্য সমস্ত বস্তুর মধ্যে দূরত্ব তাও এই গাণিতিক গতিবিদ্যা দ্বারা নির্ধারিত হয়৷
তাত্ত্বিক দিক
Titius-Bode নিয়মের অন্তর্নিহিত কোন দৃঢ় তাত্ত্বিক ব্যাখ্যা নেই, তবে এটা সম্ভব যে কক্ষপথের অনুরণন এবং স্বাধীনতার ডিগ্রির অভাবের সংমিশ্রণে, যে কোনও স্থিতিশীল গ্রহ ব্যবস্থায় বর্ণিত মডেলের পুনরাবৃত্তি হওয়ার উচ্চ সম্ভাবনা রয়েছে দুই বিজ্ঞানীর এই তত্ত্ব।
কারণ এটি একটি গাণিতিক কাকতালীয় হতে পারে এবং "প্রকৃতির নিয়ম" নয়, এটিকে কখনও কখনও "আইন" না বলে একটি নিয়ম বলা হয়। যাইহোক, জ্যোতির্পদার্থবিদ অ্যালান বস যুক্তি দেন যে এটি সহজকাকতালীয় ঘটনা, এবং প্ল্যানেটারি সায়েন্স জার্নাল ইকারাস আর "আইনের" উন্নত সংস্করণ প্রদানের চেষ্টা করে এমন নিবন্ধ গ্রহণ করছে না।
অরবিটাল রেজোন্যান্স
প্রধান প্রদক্ষিণকারী সংস্থাগুলির অরবিটাল অনুরণন সূর্যের চারপাশে এমন অঞ্চল তৈরি করে যেখানে দীর্ঘমেয়াদী স্থিতিশীল কক্ষপথ নেই। গ্রহ গঠনের সিমুলেশন ফলাফল এই ধারণাটিকে সমর্থন করে যে একটি এলোমেলোভাবে নির্বাচিত স্থিতিশীল গ্রহ ব্যবস্থা টিটিয়াস-বোড নিয়মকে সন্তুষ্ট করতে পারে৷

Dubrulle এবং Graner
ডুব্রুল এবং গ্রেনার দেখিয়েছেন যে পাওয়ার-আইন দূরত্বের নিয়মগুলি দুটি প্রতিসাম্যযুক্ত গ্রহের সিস্টেমের ধসে পড়া মেঘের মডেলগুলির পরিণতি হতে পারে: ঘূর্ণনগত বৈষম্য (মেঘ এবং এর বিষয়বস্তু অক্ষ প্রতিসম) এবং স্কেল বৈষম্য (ক্লাউড এবং এর বিষয়বস্তু সব স্কেলে একই দেখায়)।
পরবর্তীটি অনেক ঘটনার একটি বৈশিষ্ট্য যা গ্রহ গঠনে ভূমিকা পালন করে বলে মনে করা হয়, যেমন অশান্তি। টিটিয়াস এবং বোডে দ্বারা প্রস্তাবিত সৌরজগতের গ্রহগুলির সূর্য থেকে দূরত্ব, ডুব্রুল এবং গ্রেনারের গবেষণার কাঠামোতে সংশোধিত হয়নি৷






