গণিতে, যোগফল (বৃহৎ গ্রীক সিগমা চিহ্ন দ্বারা চিহ্নিত) হল সংখ্যার যোগফলের একটি সেট। পরিমাণ কত? এটি এমন একটি কর্মের ফল। যদি বাম থেকে ডানে একের পর এক সংখ্যা যোগ করা হয়, তাহলে মধ্যবর্তী ফলাফল একটি আংশিক যোগফল।
পরিমাণ কত?
সংখ্যার যোগফল পূর্ণসংখ্যা, মূলদ, বাস্তব বা জটিল হতে পারে। এগুলি ছাড়াও, অন্যান্য ধরণের মানগুলি যোগ করা যেতে পারে: ভেক্টর, ম্যাট্রিক্স, বহুপদ এবং যেকোনো সংযোজক গোষ্ঠীর সাধারণ উপাদান (বা এমনকি একটি মনোয়েড)।
যদি পদগুলির উপাদানের সংখ্যা সীমিত হয়, তাহলে সমষ্টি সর্বদা একটি সু-সংজ্ঞায়িত মান দেয়। মানের অসীম অনুক্রমের সমষ্টিকে সিরিজ বলা হয়। এর মান প্রায়শই একটি সীমা ব্যবহার করে নির্ধারণ করা যেতে পারে (যদিও কখনও কখনও মান অসীম হতে পারে)।
ক্রম
সংখ্যার যোগফল [3, 7, 2, 1] এমন একটি রাশি দ্বারা সংজ্ঞায়িত করা যেতে পারে যার মান এতে অন্তর্ভুক্ত অঙ্কগুলির যোগফল, উদাহরণস্বরূপ 3 + 7 + 2 + 1=13। যেহেতু যোগসমষ্টিগতভাবে, যোগফল কীভাবে পদগুলিকে গোষ্ঠীভুক্ত করা হয় তার উপর নির্ভর করে না, উদাহরণস্বরূপ, (3 + 7) + (2 + 1) এবং 3 + ((7 + 2) + 1) উভয়ই নয়টির সমান, তাই বন্ধনী সাধারণত dispensed with যোগও কম্যুটেটিভ, তাই পদগুলিকে পুনর্বিন্যাস করলে যোগফলের মান পরিবর্তন হয় না। মনে রাখবেন এই সম্পত্তি অসীম যোগফলের জন্য কাজ নাও করতে পারে।

এই ধরণের সিকোয়েন্স যোগ করার জন্য কোন বিশেষ নোটেশন নেই। দুটি উপাদানের কম থাকলেই সামান্য সূক্ষ্মতা আছে। এক সদস্যের একটি ক্রম-এর সমষ্টিতে একটি যোগ চিহ্ন থাকে না (এটি সংখ্যার আকার থেকে আলাদা করা যায় না), এবং যদি কোনও উপাদানই না থাকে তবে এটি লেখাও যাবে না (কিন্তু পরিবর্তে এটি দ্বারা চিহ্নিত করা যেতে পারে এর মান "0")। যাইহোক, যদি অনুক্রমের শর্তাবলী একটি নির্দিষ্ট প্যাটার্ন দ্বারা নির্দিষ্ট করা হয়, যেমন একটি ফাংশন, তাহলে যোগফল অপারেটর দরকারী বা এমনকি অপরিহার্যও হতে পারে৷
রেকর্ড
একটি যোগফল কী তা বোঝার জন্য, এটির চেহারাটিও বিশ্লেষণ করা প্রয়োজন।
1 থেকে 100 পর্যন্ত পূর্ণসংখ্যার একটি ক্রম যোগ করতে, একটি অভিব্যক্তি প্রায়শই ব্যবহৃত হয় যাতে অনুপস্থিত সদস্যদের নির্দেশ করার জন্য একটি উপবৃত্ত অন্তর্ভুক্ত থাকে: 1 + 2 + 3 + 4 + … + 99 + 100। প্যাটার্নটি হল এই উদাহরণে দেখতে মোটামুটি সহজ. যাইহোক, আরও জটিল বিকল্পগুলির জন্য, উপাদানগুলির মান খুঁজে বের করার জন্য ব্যবহৃত নিয়মটি নির্দিষ্ট করা প্রয়োজন, যা "Σ" যোগফল অপারেটর ব্যবহার করে অর্জন করা যেতে পারে। এই প্রতীক (সিগমা) ব্যবহার করে, আপনি নিম্নলিখিত স্বরলিপি প্রয়োগ করতে পারেন:
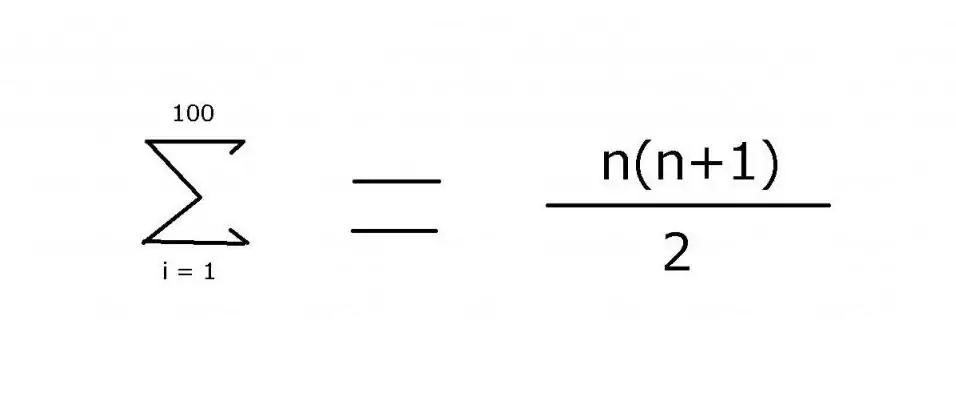
এই রাশিটির মান হল 5050। এটি গাণিতিক ইন্ডাকশন ব্যবহার করে পাওয়া যাবে, যেখান থেকে সূত্রের দ্বিতীয় অংশটি এসেছে।
বিভিন্ন অনুক্রমের জন্য, সূত্র পরিবর্তন হবে। রেকর্ডিং প্রক্রিয়াটি কিছু অসীম অনুক্রমের প্রাক-ইমেজ অনুসন্ধান এবং তারপর একটি সূত্র দিয়ে বর্ণনা করার জন্য হ্রাস করা হয়। এটি করার পরে, একটি নির্দিষ্ট ক্ষেত্রে পরিমাণটি কী তা বোঝা কঠিন নয়।
যখন এটা স্পষ্ট করার প্রয়োজন হয় যে সংখ্যাগুলিকে তাদের চিহ্নের (প্লাস বা বিয়োগ) সাথে একত্রে যুক্ত করা হয়, তখন বীজগণিতের যোগফল শব্দটি ব্যবহার করা হয়। উদাহরণ স্বরূপ, বৈদ্যুতিক সার্কিট তত্ত্বে, কিরচফের সার্কিট আইনগুলি একটি বিন্দুতে মিলিত কন্ডাক্টর নেটওয়ার্কে স্রোতের বীজগাণিতিক যোগফলকে বিবেচনা করে, যা একটি নোডের মধ্যে এবং বাইরে প্রবাহিত স্রোতের বিপরীত লক্ষণ দেয়৷






