ওহমের সূত্র হল বৈদ্যুতিক সার্কিটের মৌলিক সূত্র। একই সময়ে, এটি আমাদের অনেক প্রাকৃতিক ঘটনা ব্যাখ্যা করতে দেয়। উদাহরণস্বরূপ, কেউ বুঝতে পারে কেন বিদ্যুৎ তারের উপর বসে থাকা পাখিদের "বীট" করে না। পদার্থবিজ্ঞানের জন্য, ওহমের সূত্র অত্যন্ত তাৎপর্যপূর্ণ। তার জ্ঞান ছাড়া, স্থিতিশীল বৈদ্যুতিক সার্কিট তৈরি করা অসম্ভব হবে বা সেখানে কোনো ইলেকট্রনিক্স থাকবে না।
নির্ভরতা I=I(U) এবং এর মান
পদার্থের প্রতিরোধের আবিষ্কারের ইতিহাস সরাসরি বর্তমান-ভোল্টেজ বৈশিষ্ট্যের সাথে সম্পর্কিত। এটা কি? চলুন একটি স্থির বৈদ্যুতিক প্রবাহ সহ একটি সার্কিট গ্রহণ করি এবং এর যে কোনো উপাদান বিবেচনা করি: একটি বাতি, একটি গ্যাস পাইপ, একটি ধাতব পরিবাহী, একটি ইলেক্ট্রোলাইট ফ্লাস্ক ইত্যাদি।
প্রশ্নে থাকা উপাদানটিতে সরবরাহ করা ভোল্টেজ U (প্রায়শই V হিসাবে উল্লেখ করা হয়) পরিবর্তন করে, আমরা এটির মধ্য দিয়ে যাওয়া কারেন্ট (I) এর শক্তির পরিবর্তন ট্র্যাক করব। ফলস্বরূপ, আমরা I \u003d I (U) ফর্মের একটি নির্ভরতা পাব, যাকে "উপাদানের ভোল্টেজ বৈশিষ্ট্য" বলা হয় এবং এটি এর সরাসরি নির্দেশক।বৈদ্যুতিক বৈশিষ্ট্য।
V/একটি বৈশিষ্ট্য বিভিন্ন উপাদানের জন্য আলাদা দেখতে হতে পারে। এটির সহজতম রূপটি একটি ধাতব পরিবাহী বিবেচনা করে পাওয়া যায়, যা জর্জ ওহম (1789 - 1854) করেছিলেন।
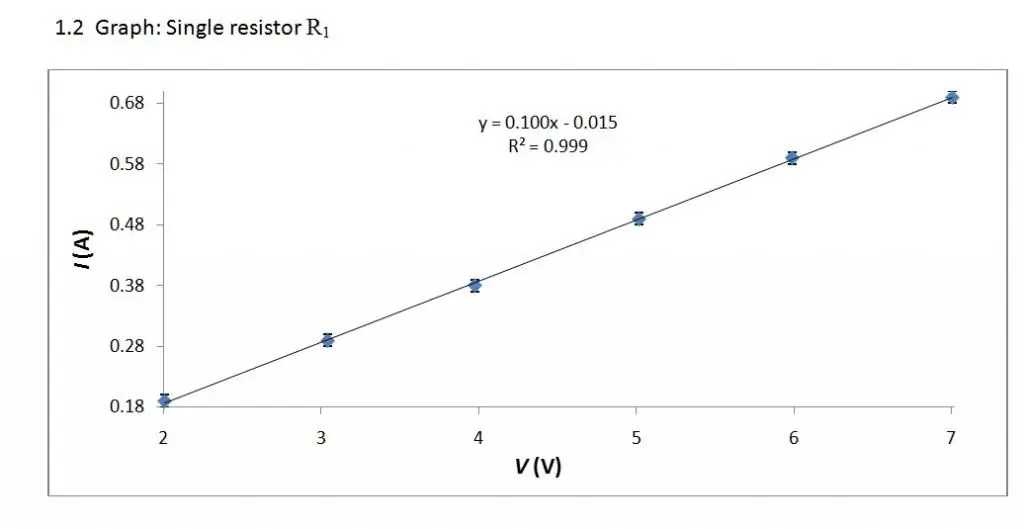
ভোল্ট-অ্যাম্পিয়ার বৈশিষ্ট্য একটি রৈখিক সম্পর্ক। অতএব, এর গ্রাফ একটি সরল রেখা।
আইন তার সহজতম আকারে
পরিবাহীর বর্তমান-ভোল্টেজ বৈশিষ্ট্যের উপর ওহমের গবেষণায় দেখা গেছে যে একটি ধাতব পরিবাহীর ভিতরে বর্তমান শক্তি তার প্রান্তে সম্ভাব্য পার্থক্যের সমানুপাতিক (I ~ U) এবং একটি নির্দিষ্ট সহগের বিপরীতভাবে সমানুপাতিক, অর্থাৎ, I ~ 1/আর. এই সহগটি "পরিবাহী প্রতিরোধ" হিসাবে পরিচিত হয় এবং বৈদ্যুতিক প্রতিরোধের পরিমাপের একক ছিল ওহম বা V/A।
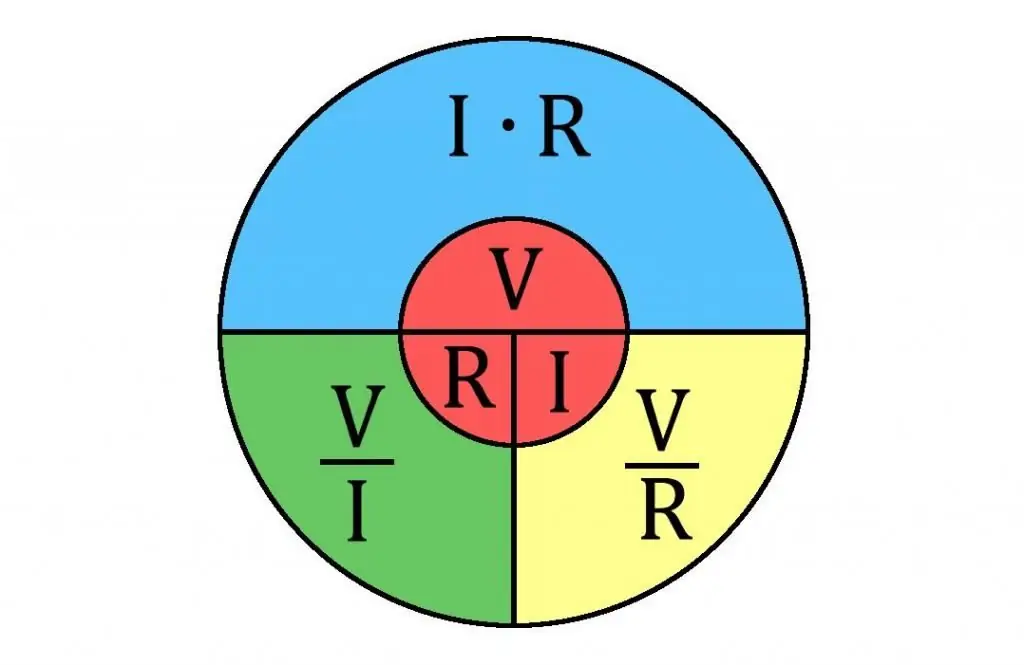
আরো একটি জিনিস লক্ষ্য করুন। ওহমের সূত্র প্রায়শই সার্কিটে প্রতিরোধের গণনা করতে ব্যবহৃত হয়।
আইন শব্দচয়ন
ওহমের সূত্র বলে যে সার্কিটের একটি একক অংশের বর্তমান শক্তি (I) এই বিভাগে ভোল্টেজের সমানুপাতিক এবং এর প্রতিরোধের বিপরীতভাবে সমানুপাতিক৷
এটা লক্ষ করা উচিত যে এই ফর্মে আইনটি শুধুমাত্র শৃঙ্খলের একটি সমজাতীয় অংশের জন্যই সত্য। সমজাতীয় হল বৈদ্যুতিক বর্তনীর সেই অংশ যাতে বর্তমানের উৎস থাকে না। একটি অসংলগ্ন সার্কিটে ওহমের সূত্র কীভাবে ব্যবহার করবেন তা নীচে আলোচনা করা হবে৷
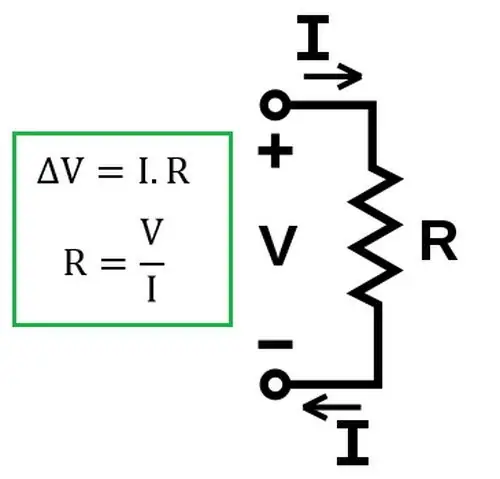
পরে, এটি পরীক্ষামূলকভাবে প্রতিষ্ঠিত হয় যে আইনটি সমাধানের জন্য বৈধবৈদ্যুতিক সার্কিটে ইলেক্ট্রোলাইটস।
প্রতিরোধের শারীরিক অর্থ
প্রতিরোধ হল বৈদ্যুতিক প্রবাহকে আটকানোর জন্য পদার্থ, পদার্থ বা মিডিয়ার একটি সম্পত্তি। পরিমাণগতভাবে, 1 ওহমের একটি প্রতিরোধের মানে হল যে একটি কন্ডাক্টরে যার প্রান্তে 1 V ভোল্টেজ রয়েছে, 1 A এর বৈদ্যুতিক প্রবাহ যেতে পারে।
বৈদ্যুতিক প্রতিরোধ ক্ষমতা
পরীক্ষামূলকভাবে, এটি পাওয়া গেছে যে পরিবাহীর বৈদ্যুতিক প্রবাহের প্রতিরোধ তার মাত্রার উপর নির্ভর করে: দৈর্ঘ্য, প্রস্থ, উচ্চতা। এবং এটির আকার (গোলক, সিলিন্ডার) এবং যে উপাদান থেকে এটি তৈরি করা হয় তার উপরও। সুতরাং, প্রতিরোধ ক্ষমতার সূত্র, উদাহরণস্বরূপ, একটি সমজাতীয় নলাকার পরিবাহী হবে: R \u003d pl / S.
এই সূত্রে যদি আমরা s=1 m2 এবং l=1 m রাখি, তাহলে R হবে সংখ্যাগতভাবে p-এর সমান। এখান থেকে, SI-তে পরিবাহীর রোধের সহগের পরিমাপের একক গণনা করা হয় - এটি ওহমমি।

রেজিসিটিভিটি সূত্রে, p হল রেজিস্ট্যান্স সহগ উপাদানের রাসায়নিক বৈশিষ্ট্য দ্বারা নির্ধারিত হয় যেখান থেকে কন্ডাকটর তৈরি হয়।
ওহমের সূত্রের ডিফারেনশিয়াল ফর্ম বিবেচনা করতে, আমাদের আরও কয়েকটি ধারণা বিবেচনা করতে হবে।
বর্তমান ঘনত্ব
আপনি জানেন যে, বৈদ্যুতিক প্রবাহ হল যে কোনো চার্জযুক্ত কণার একটি কঠোরভাবে নির্দেশিত চলাচল। উদাহরণস্বরূপ, ধাতুগুলিতে, বর্তমান বাহকগুলি ইলেকট্রন এবং গ্যাসগুলি পরিচালনার ক্ষেত্রে আয়নগুলি।
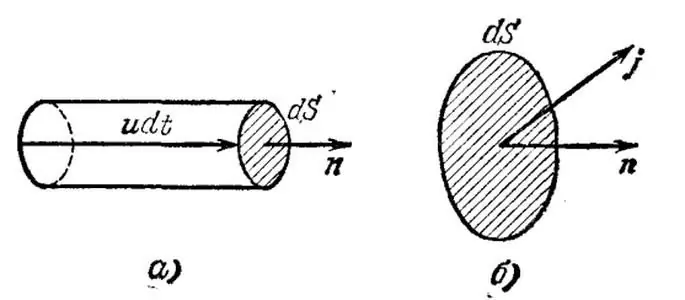
যখন সমস্ত বর্তমান বাহক তুচ্ছ ঘটনাটি নিনসমজাতীয় - ধাতু পরিবাহী। আসুন মানসিকভাবে এই পরিবাহীতে একটি অসীম ছোট আয়তনকে আলাদা করি এবং প্রদত্ত আয়তনে ইলেকট্রনের গড় (প্রবাহ, আদেশকৃত) বেগ বোঝাই। আরও, n প্রতি ইউনিট ভলিউমের বর্তমান বাহকের ঘনত্ব বোঝাই।
এখন চলুন একটি অসীম ক্ষেত্র dS লম্ব ভেক্টর u আঁকুন এবং বেগ বরাবর একটি উচ্চতা udt সহ একটি অসীম সিলিন্ডার তৈরি করি, যেখানে dt সেই সময়টিকে নির্দেশ করে যে সময়ে বিবেচিত আয়তনের মধ্যে থাকা সমস্ত বর্তমান বেগ বাহক অতিক্রম করবে এলাকা dS.
এই ক্ষেত্রে, q=neudSdt এর সমান চার্জটি ইলেকট্রন দ্বারা এলাকার মাধ্যমে স্থানান্তরিত হবে, যেখানে e হল ইলেকট্রন চার্জ। এইভাবে, বৈদ্যুতিক প্রবাহের ঘনত্ব হল একটি ভেক্টর j =neu, যা একটি ইউনিট এলাকার মাধ্যমে প্রতি ইউনিট সময় স্থানান্তরিত চার্জের পরিমাণ নির্দেশ করে৷
ওহমের ল ডিফারেনশিয়াল সংজ্ঞার একটি সুবিধা হল যে আপনি প্রায়শই প্রতিরোধের হিসাব না করেই পেতে পারেন।
ইলেকট্রিক চার্জ। বৈদ্যুতিক ক্ষেত্রের শক্তি
বৈদ্যুতিক চার্জ সহ ক্ষেত্রের শক্তি বিদ্যুতের তত্ত্বের একটি মৌলিক পরামিতি। একই সময়ে, তাদের একটি পরিমাণগত ধারণা স্কুলছাত্রীদের জন্য উপলব্ধ সহজ পরীক্ষা থেকে প্রাপ্ত করা যেতে পারে।
সরলতার জন্য, আমরা একটি ইলেক্ট্রোস্ট্যাটিক ক্ষেত্র বিবেচনা করব। এটি একটি বৈদ্যুতিক ক্ষেত্র যা সময়ের সাথে পরিবর্তিত হয় না। এই ধরনের একটি ক্ষেত্র স্থির বৈদ্যুতিক চার্জ দ্বারা তৈরি করা যেতে পারে।
এছাড়াও, আমাদের উদ্দেশ্যে একটি পরীক্ষার চার্জ প্রয়োজন৷ এর ক্ষমতায় আমরা একটি চার্জযুক্ত বডি ব্যবহার করব - এত ছোট যে এটি ঘটাতে সক্ষম নয়আশেপাশের বস্তুর মধ্যে যেকোন ঝামেলা (চার্জের পুনঃবন্টন)।
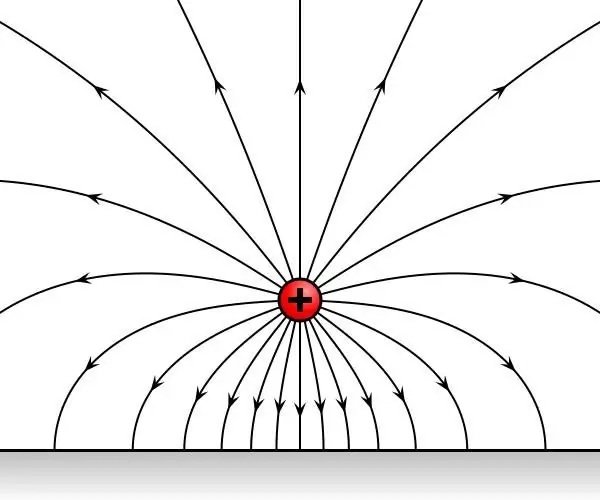
আসুন পালাক্রমে বিবেচনা করা যাক দুটি টেস্ট চার্জ নেওয়া হয়েছে, পর্যায়ক্রমে মহাকাশের এক বিন্দুতে স্থাপন করা হয়েছে, যা একটি ইলেক্ট্রোস্ট্যাটিক ক্ষেত্রের প্রভাবে রয়েছে। এটা দেখা যাচ্ছে যে অভিযোগ তার পক্ষ থেকে সময়-অপরিবর্তিত প্রভাবের অধীন হবে। F1 এবং F2 চার্জের উপর কাজ করে
পরীক্ষামূলক ডেটার সাধারণীকরণের ফলস্বরূপ, এটি পাওয়া গেছে যে F1 এবং F2 হয় এক বা বিপরীত দিকে, এবং তাদের অনুপাত F1/F2 স্থানের বিন্দু থেকে স্বতন্ত্র যেখানে পরীক্ষা চার্জগুলি পর্যায়ক্রমে স্থাপন করা হয়েছিল। অতএব, অনুপাত F1/F2 চার্জের একটি বৈশিষ্ট্য এবং এটি ক্ষেত্রের উপর নির্ভর করে না৷
এই সত্যটি আবিষ্কারের ফলে দেহের বৈদ্যুতিককরণের বৈশিষ্ট্য চিহ্নিত করা সম্ভব হয়েছিল এবং পরে একে বৈদ্যুতিক চার্জ বলা হয়। সুতরাং, সংজ্ঞা অনুসারে, এটি q1/q2=F1/F 2 , যেখানে q1 এবং q2 - ক্ষেত্রের এক বিন্দুতে চার্জের পরিমাণ এবং F 1 এবং F2 - ক্ষেত্রের দিক থেকে চার্জের উপর কাজ করছে।
এই ধরনের বিবেচনা থেকে, বিভিন্ন কণার চার্জের মাত্রা পরীক্ষামূলকভাবে প্রতিষ্ঠিত হয়েছিল। শর্তসাপেক্ষে একটি পরীক্ষা চার্জের একটি অনুপাতের সমান সেট করে, আপনি F1/F2 অনুপাত পরিমাপ করে অন্য চার্জের মান গণনা করতে পারেন.
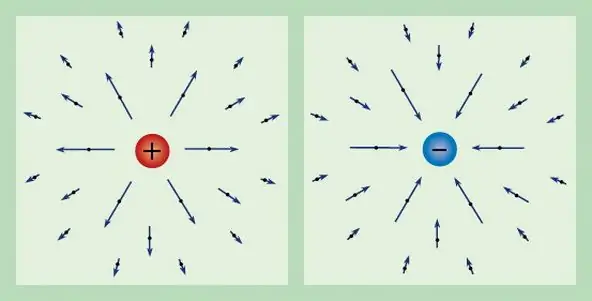
যেকোন বৈদ্যুতিক ক্ষেত্র একটি পরিচিত চার্জের মাধ্যমে চিহ্নিত করা যেতে পারে। সুতরাং, বিশ্রামে একটি ইউনিট টেস্ট চার্জের উপর যে বল কাজ করে তাকে বৈদ্যুতিক ক্ষেত্রের শক্তি বলা হয় এবং E দ্বারা চিহ্নিত করা হয়। চার্জের সংজ্ঞা থেকে, আমরা পাই যে শক্তি ভেক্টরের নিম্নলিখিত রূপ রয়েছে: E=F/q.
j এবং E ভেক্টরের সংযোগ। ওহমের সূত্রের আরেকটি রূপ
একটি সমজাতীয় পরিবাহীতে, আধানযুক্ত কণার নির্দেশিত গতি ভেক্টর E এর দিকে ঘটবে। এর মানে হল j এবং E ভেক্টরগুলি সহ-নির্দেশিত হবে। বর্তমান ঘনত্ব নির্ধারণের মতো, আমরা কন্ডাকটরে একটি অসীম ছোট নলাকার ভলিউম নির্বাচন করি। তারপর jdS এর সমান একটি কারেন্ট এই সিলিন্ডারের ক্রস সেকশনের মধ্য দিয়ে যাবে এবং সিলিন্ডারে প্রয়োগ করা ভোল্টেজটি Edl এর সমান হবে। একটি সিলিন্ডারের রোধের সূত্রটিও জানা যায়৷
তারপর, বর্তমান শক্তির সূত্রটি দুটি উপায়ে লিখলে, আমরা পাই: j=E/p, যেখানে মান 1/p কে বৈদ্যুতিক পরিবাহিতা বলা হয় এবং এটি বৈদ্যুতিক প্রতিরোধের বিপরীত। এটি সাধারণত σ (সিগমা) বা λ (ল্যাম্বডা) চিহ্নিত করা হয়। পরিবাহিতার একক হল Sm/m, যেখানে Sm হল সিমেন্স। ওহমের একক বিপরীত।
এইভাবে, আমরা একটি অসংলগ্ন সার্কিটের জন্য ওহমের সূত্র সম্পর্কে উপরে উত্থাপিত প্রশ্নের উত্তর দিতে পারি। এই ক্ষেত্রে, বর্তমান বাহকগুলি ইলেক্ট্রোস্ট্যাটিক ক্ষেত্রের শক্তি দ্বারা প্রভাবিত হবে, যা তীব্রতা E1 দ্বারা চিহ্নিত করা হয়, এবং অন্যান্য শক্তিগুলি অন্য বর্তমান উত্স থেকে তাদের উপর কাজ করে, যা হতে পারে মনোনীত E 2. তারপর ওহমের আইন প্রয়োগ করা হয়শৃঙ্খলের অসঙ্গতিপূর্ণ অংশটি এরকম দেখাবে: j=λ(E1 + E2)।
পরিবাহিতা এবং প্রতিরোধ সম্পর্কে আরও
একটি কন্ডাক্টরের বৈদ্যুতিক প্রবাহ পরিচালনা করার ক্ষমতা তার প্রতিরোধ ক্ষমতা দ্বারা চিহ্নিত করা হয়, যা পরিবাহিতার পারস্পরিক হিসাবে গণনা করা প্রতিরোধক সূত্র বা পরিবাহিতা দ্বারা পাওয়া যায়। এই পরামিতিগুলির মান কন্ডাকটর উপাদানের রাসায়নিক বৈশিষ্ট্য এবং বাহ্যিক অবস্থার দ্বারা উভয়ই নির্ধারিত হয়। বিশেষ করে, পরিবেষ্টিত তাপমাত্রা।
অধিকাংশ ধাতুর জন্য, স্বাভাবিক তাপমাত্রায় প্রতিরোধ ক্ষমতা এর সমানুপাতিক, অর্থাৎ p ~ T। যাইহোক, নিম্ন তাপমাত্রায় বিচ্যুতি পরিলক্ষিত হয়। 0°K এর কাছাকাছি তাপমাত্রায় প্রচুর সংখ্যক ধাতু এবং সংকর ধাতুর জন্য, প্রতিরোধের গণনা শূন্য মান দেখায়। এই ঘটনাকে বলা হয় সুপারকন্ডাক্টিভিটি। উদাহরণস্বরূপ, পারদ, টিন, সীসা, অ্যালুমিনিয়াম ইত্যাদির এই বৈশিষ্ট্য রয়েছে। প্রতিটি ধাতুর নিজস্ব গুরুত্বপূর্ণ তাপমাত্রা রয়েছে Tk, যেখানে অতিপরিবাহীতার ঘটনাটি পরিলক্ষিত হয়।
এছাড়াও মনে রাখবেন যে সিলিন্ডার প্রতিরোধের সংজ্ঞাটি একই উপাদান দিয়ে তৈরি তারগুলিতে সাধারণীকরণ করা যেতে পারে। এই ক্ষেত্রে, রেজিসিটিভিটি সূত্র থেকে ক্রস-বিভাগীয় এলাকা হবে তারের ক্রস সেকশনের সমান, এবং l - এর দৈর্ঘ্য।






