ডিফারেনশিয়াল এবং অখণ্ড আকারে ওহমের সূত্রে বলা হয়েছে যে দুটি বিন্দুর মধ্যে একটি পরিবাহীর মাধ্যমে প্রবাহটি দুটি বিন্দুতে ভোল্টেজের সরাসরি সমানুপাতিক। ধ্রুবক সহ একটি সমীকরণ এইরকম দেখায়:
I=V/R, যেখানে আমি অ্যাম্পিয়ারের এককগুলিতে পরিবাহীর মাধ্যমে কারেন্টের বিন্দু, V (ভোল্ট) হল ভোল্টের এককগুলিতে পরিবাহী দিয়ে পরিমাপ করা ভোল্টেজ, R হল ওহমে সঞ্চালিত উপাদানটির প্রতিরোধ। আরও বিশেষভাবে, ওহমের সূত্র বলে যে R এই ক্ষেত্রে একটি ধ্রুবক, কারেন্ট থেকে স্বাধীন।
"ওহমের সূত্র" দ্বারা কী বোঝা যায়?
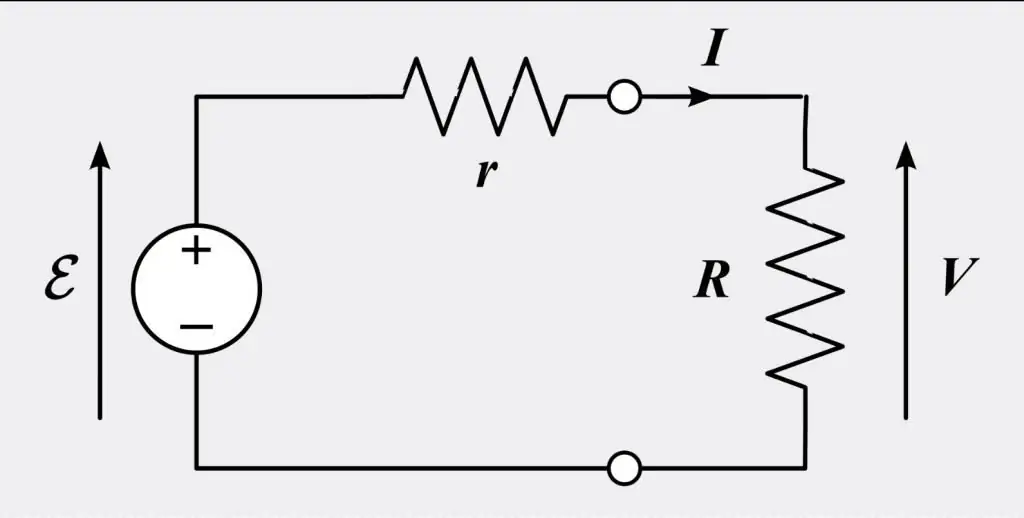
ডিফারেনশিয়াল এবং অবিচ্ছেদ্য আকারে ওহমের আইন হল একটি অভিজ্ঞতামূলক সম্পর্ক যা বেশিরভাগ পরিবাহী পদার্থের পরিবাহিতাকে সঠিকভাবে বর্ণনা করে। যাইহোক, কিছু উপকরণ ওহমের আইন মানে না, তাদের বলা হয় "ননওমিক"। আইনটির নামকরণ করা হয়েছিল বিজ্ঞানী জর্জ ওহমের নামে, যিনি এটি 1827 সালে প্রকাশ করেছিলেন। এটি সাধারণ বৈদ্যুতিক সার্কিট ধারণকারী ব্যবহার করে ভোল্টেজ এবং বর্তমান পরিমাপ বর্ণনা করেবিভিন্ন তারের দৈর্ঘ্য। ওহম তার পরীক্ষামূলক ফলাফলকে উপরের আধুনিক ফর্মের চেয়ে একটু বেশি জটিল সমীকরণ দিয়ে ব্যাখ্যা করেছেন।
অহমের সূত্রের ধারণা ভিন্ন। ফর্মটি বিভিন্ন সাধারণীকরণ বোঝাতেও ব্যবহৃত হয়, উদাহরণস্বরূপ, এর ভেক্টর ফর্ম ইলেক্ট্রোম্যাগনেটিজম এবং পদার্থ বিজ্ঞানে ব্যবহৃত হয়:
J=σE, যেখানে J হল প্রতিরোধক পদার্থের একটি নির্দিষ্ট স্থানে বৈদ্যুতিক কণার সংখ্যা, e হল সেই অবস্থানের বৈদ্যুতিক ক্ষেত্র এবং σ (সিগমা) হল পরিবাহিতা পরামিতির উপর নির্ভরশীল উপাদান। গুস্তাভ কির্চহফ ঠিক এভাবেই আইন প্রণয়ন করেছিলেন।
ইতিহাস

ইতিহাস
1781 সালের জানুয়ারিতে, হেনরি ক্যাভেন্ডিশ একটি লেইডেন জার এবং লবণের দ্রবণে ভরা বিভিন্ন ব্যাসের একটি গ্লাস টিউব নিয়ে পরীক্ষা করেন। ক্যাভেন্ডিশ লিখেছেন যে গতি সরাসরি বিদ্যুতায়নের মাত্রা হিসাবে পরিবর্তিত হয়। প্রাথমিকভাবে, ফলাফলগুলি বৈজ্ঞানিক সম্প্রদায়ের কাছে অজানা ছিল। কিন্তু ম্যাক্সওয়েল 1879 সালে সেগুলো প্রকাশ করেন।
ওহম 1825 এবং 1826 সালে প্রতিরোধের উপর তার কাজ করেছিলেন এবং 1827 সালে "দ্য গ্যালভানিক সার্কিট গাণিতিকভাবে প্রমাণিত"-এ তার ফলাফল প্রকাশ করেছিলেন। তিনি ফরাসি গণিতবিদ ফুরিয়ারের কাজ দ্বারা অনুপ্রাণিত হয়েছিলেন, যিনি তাপ সঞ্চালনের বর্ণনা করেছিলেন। পরীক্ষার জন্য, তিনি প্রাথমিকভাবে গ্যালভানিক পাইলস ব্যবহার করেছিলেন, কিন্তু পরে থার্মোকলগুলিতে স্যুইচ করেছিলেন, যা আরও স্থিতিশীল ভোল্টেজের উত্স সরবরাহ করতে পারে। তিনি অভ্যন্তরীণ প্রতিরোধ এবং ধ্রুবক ভোল্টেজের ধারণা নিয়ে কাজ করেছিলেন।
এছাড়াও এই পরীক্ষাগুলিতে, একটি গ্যালভানোমিটার কারেন্ট পরিমাপ করতে ব্যবহৃত হয়েছিল, যেহেতু ভোল্টেজসংযোগ তাপমাত্রার সমানুপাতিক থার্মোকল টার্মিনালের মধ্যে। তারপর তিনি সার্কিটটি সম্পূর্ণ করার জন্য বিভিন্ন দৈর্ঘ্য, ব্যাস এবং উপকরণের পরীক্ষামূলক লিড যোগ করেন। তিনি দেখেছেন যে তার ডেটা নিম্নলিখিত সমীকরণের সাথে মডেল করা যেতে পারে
x=a /b + l, যেখানে x হল মিটার রিডিং, l হল পরীক্ষার সীসার দৈর্ঘ্য, a থার্মোকল জংশনের তাপমাত্রার উপর নির্ভরশীল, b হল পুরো সমীকরণের একটি ধ্রুবক (ধ্রুবক)। ওহম এই আনুপাতিকতার গণনার উপর ভিত্তি করে তার আইন প্রমাণ করেছে এবং তার ফলাফল প্রকাশ করেছে।
ওহমের সূত্রের গুরুত্ব
ডিফারেনশিয়াল এবং অবিচ্ছেদ্য আকারে ওহমের সূত্র সম্ভবত বিদ্যুতের পদার্থবিদ্যার প্রাথমিক বর্ণনার মধ্যে সবচেয়ে গুরুত্বপূর্ণ ছিল। আজ আমরা এটিকে প্রায় সুস্পষ্ট বিবেচনা করি, কিন্তু ওম যখন প্রথম তার কাজ প্রকাশ করেন, তখন এটি ছিল না। সমালোচকরা শত্রুতার সাথে তার ব্যাখ্যার প্রতিক্রিয়া জানিয়েছেন। তারা তার কাজকে "নগ্ন কল্পনা" বলে অভিহিত করেছেন এবং জার্মান শিক্ষামন্ত্রী ঘোষণা করেছেন যে "যে অধ্যাপক এই ধরনের ধর্মদ্রোহিতা প্রচার করেন তিনি বিজ্ঞান শেখানোর অযোগ্য।"
জার্মানিতে সেই সময়ে প্রচলিত বৈজ্ঞানিক দর্শন মনে করেছিল যে প্রকৃতি সম্পর্কে বোঝার জন্য পরীক্ষা-নিরীক্ষার প্রয়োজন ছিল না। এছাড়াও, Geogr এর ভাই, মার্টিন, পেশায় একজন গণিতবিদ, জার্মান শিক্ষা ব্যবস্থার সাথে লড়াই করেছিলেন। এই কারণগুলি ওহমের কাজের গ্রহণযোগ্যতাকে বাধা দেয় এবং তার কাজ 1840 সাল পর্যন্ত ব্যাপকভাবে গৃহীত হয়নি। তবুও, ওম তার মৃত্যুর অনেক আগে বিজ্ঞানে তার অবদানের জন্য স্বীকৃতি পেয়েছিলেন।
ডিফারেনশিয়াল এবং অখণ্ড আকারে ওহমের সূত্র একটি অভিজ্ঞতামূলক আইন,অনেক পরীক্ষা-নিরীক্ষার ফলাফলের সাধারণীকরণ, যা দেখায় যে কারেন্ট বেশিরভাগ উপকরণের জন্য বৈদ্যুতিক ক্ষেত্রের ভোল্টেজের প্রায় সমানুপাতিক। এটি ম্যাক্সওয়েলের সমীকরণের চেয়ে কম মৌলিক এবং সব পরিস্থিতিতে উপযুক্ত নয়। যে কোনো উপাদান পর্যাপ্ত বৈদ্যুতিক ক্ষেত্রের বলের অধীনে ভেঙ্গে যাবে।
ওহমের সূত্র বিস্তৃত আকারে পরিলক্ষিত হয়েছে। 20 শতকের শুরুতে, ওহমের সূত্রকে পারমাণবিক স্কেলে বিবেচনা করা হয়নি, কিন্তু পরীক্ষাগুলি এর বিপরীতটি নিশ্চিত করে।
কোয়ান্টাম শুরু
প্রয়োগিত বৈদ্যুতিক ক্ষেত্রের উপর বর্তমান ঘনত্বের নির্ভরতার একটি মৌলিকভাবে কোয়ান্টাম-যান্ত্রিক চরিত্র (ধ্রুপদী কোয়ান্টাম ব্যাপ্তিযোগ্যতা) রয়েছে। 1900 সালে জার্মান পদার্থবিদ পল ড্রুডের তৈরি ড্রুড মডেল ব্যবহার করে ওহমের আইনের একটি গুণগত বর্ণনা ক্লাসিক্যাল মেকানিক্সের উপর ভিত্তি করে করা যেতে পারে। এই কারণে, ওহমের সূত্রের অনেক রূপ রয়েছে, যেমন তথাকথিত ওহমের সূত্র ডিফারেনশিয়াল আকারে।
ওহমের সূত্রের অন্যান্য রূপ
ডিফারেনশিয়াল আকারে ওহমের সূত্রটি বৈদ্যুতিক/ইলেকট্রনিক্স ইঞ্জিনিয়ারিংয়ের একটি অত্যন্ত গুরুত্বপূর্ণ ধারণা কারণ এটি ভোল্টেজ এবং প্রতিরোধ উভয়কেই বর্ণনা করে। এই সমস্ত ম্যাক্রোস্কোপিক স্তরে আন্তঃসংযুক্ত। ম্যাক্রো- বা মাইক্রোস্কোপিক স্তরে বৈদ্যুতিক বৈশিষ্ট্যগুলি অধ্যয়ন করার সময়, একটি আরও সম্পর্কিত সমীকরণ ব্যবহার করা হয়, যাকে "ওহমের সমীকরণ" বলা যেতে পারে, যার ভেরিয়েবলগুলি রয়েছে যা ওহমের সূত্রের স্কেলার ভেরিয়েবল V, I, এবং R এর সাথে ঘনিষ্ঠভাবে সম্পর্কিত, কিন্তু যা মধ্যে অবস্থানের একটি ধ্রুবক ফাংশনএক্সপ্লোরার।
চুম্বকত্বের প্রভাব

যদি একটি বাহ্যিক চৌম্বক ক্ষেত্র (B) উপস্থিত থাকে এবং কন্ডাকটরটি বিশ্রামে না থাকে তবে V গতিতে চলে, তাহলে চার্জে লরেন্টজ বল দ্বারা প্রবর্তিত বর্তমানের জন্য একটি অতিরিক্ত পরিবর্তনশীল যোগ করতে হবে বাহক অখণ্ড রূপের ওহমের সূত্রও বলা হয়:
J=σ (E + vB)।
একটি চলমান পরিবাহীর বিশ্রামের ফ্রেমে, এই শব্দটি বাদ দেওয়া হয় কারণ V=0। কোন প্রতিরোধ নেই কারণ বিশ্রামের ফ্রেমের বৈদ্যুতিক ক্ষেত্র পরীক্ষাগার ফ্রেমের ই-ক্ষেত্র থেকে আলাদা: E'=E + v × B. বৈদ্যুতিক এবং চৌম্বক ক্ষেত্র আপেক্ষিক। যদি J (কারেন্ট) পরিবর্তনশীল হয় কারণ প্রয়োগকৃত ভোল্টেজ বা ই-ক্ষেত্র সময়ের সাথে পরিবর্তিত হয়, তাহলে সেলফ-ইন্ডাকশনের জন্য অ্যাকাউন্টের প্রতিরোধের সাথে বিক্রিয়া যোগ করতে হবে। ফ্রিকোয়েন্সি বেশি হলে বা পরিবাহী ক্ষত হলে বিক্রিয়া শক্তিশালী হতে পারে।






