পদার্থবিজ্ঞানে, সমান্তরাল এবং সিরিজ সংযোগের বিষয়টি অধ্যয়ন করা হয় এবং এটি কেবল পরিবাহী নয়, ক্যাপাসিটারও হতে পারে। তাদের প্রত্যেকটি ডায়াগ্রামে কেমন দেখাচ্ছে সে সম্পর্কে বিভ্রান্ত না হওয়া এখানে গুরুত্বপূর্ণ। এবং শুধুমাত্র তারপর নির্দিষ্ট সূত্র প্রয়োগ করুন। যাইহোক, আপনাকে তাদের হৃদয় দিয়ে মনে রাখতে হবে।
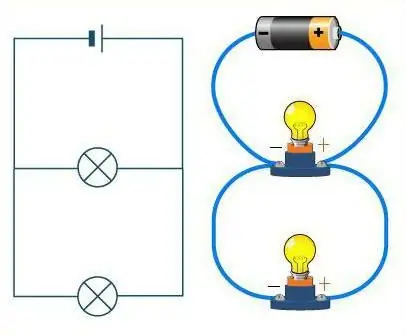
এই দুটি যৌগের মধ্যে কীভাবে পার্থক্য করা যায়?
চিত্রটি ঘনিষ্ঠভাবে দেখুন। যদি তারগুলি একটি রাস্তা হিসাবে উপস্থাপিত হয়, তবে এটির গাড়িগুলি প্রতিরোধকের ভূমিকা পালন করবে। কোনো কাঁটাবিহীন সোজা রাস্তায়, গাড়িগুলো একটার পর একটা চেইন দিয়ে চলে। কন্ডাক্টরের সিরিজ সংযোগও একই রকম দেখায়। এই ক্ষেত্রে রাস্তাটিতে সীমাহীন সংখ্যক বাঁক থাকতে পারে, তবে একটি ছেদ নয়। রাস্তা (তারের) যেভাবে নাড়াচাড়া করুক না কেন, মেশিন (প্রতিরোধক) সবসময় একের পর এক, এক শৃঙ্খলে অবস্থান করবে।
একটি সমান্তরাল সংযোগ বিবেচনা করা হলে এটি সম্পূর্ণ ভিন্ন বিষয়। তারপর প্রতিরোধকারীদের শুরুতে ক্রীড়াবিদদের সাথে তুলনা করা যেতে পারে। তারাপ্রতিটি তার নিজস্ব ট্র্যাকে স্ট্যান্ড, কিন্তু তাদের চলাচলের একই দিক রয়েছে এবং ফিনিস লাইন একই জায়গায় রয়েছে। একইভাবে, প্রতিরোধক - তাদের প্রত্যেকের নিজস্ব তার আছে, কিন্তু তারা সবগুলোই কোনো না কোনো সময়ে সংযুক্ত থাকে।
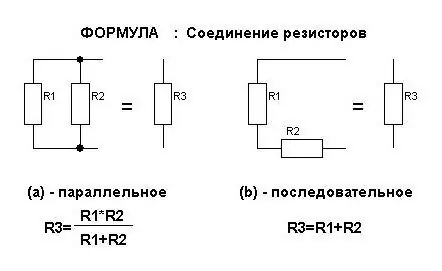
বর্তমান শক্তির সূত্র
এটি সর্বদা "বিদ্যুত" বিষয়ে আলোচনা করা হয়। সমান্তরাল এবং সিরিজ সংযোগ বিভিন্ন উপায়ে প্রতিরোধক মধ্যে বর্তমান পরিমাণ প্রভাবিত করে। তাদের জন্য, সূত্রগুলি উদ্ভূত হয় যা মনে রাখা যেতে পারে। কিন্তু তাদের মধ্যে যে অর্থ বিনিয়োগ করা হয়েছে তা মনে রাখাই যথেষ্ট।
সুতরাং, কন্ডাক্টরের সিরিজ সংযোগে কারেন্ট সবসময় একই থাকে। অর্থাৎ, তাদের প্রতিটিতে বর্তমান শক্তির মান আলাদা নয়। যদি আপনি একটি পাইপের সাথে একটি তারের তুলনা করেন তবে আপনি একটি সাদৃশ্য আঁকতে পারেন। এটিতে, জল সর্বদা একইভাবে প্রবাহিত হয়। এবং এর পথের সমস্ত বাধা একই শক্তিতে ভেসে যাবে। কারেন্টের সাথে একই। অতএব, প্রতিরোধকের সিরিজ সংযোগ সহ একটি সার্কিটে মোট কারেন্টের সূত্রটি এইরকম দেখায়:
I জেন=আমি 1=আমি 2
এখানে, আমি যে অক্ষরটি স্রোতের শক্তি বোঝায় তা বোঝায়। এটি একটি সাধারণ স্বরলিপি, তাই আপনাকে এটি মনে রাখতে হবে৷
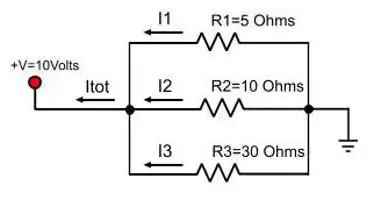
সমান্তরাল সংযোগে বর্তমান আর একটি ধ্রুবক মান হবে না। একটি পাইপের সাথে একই সাদৃশ্যের সাথে, এটি দেখা যাচ্ছে যে প্রধান পাইপের একটি শাখা থাকলে জল দুটি প্রবাহে বিভক্ত হবে। একই ঘটনাটি কারেন্টের সাথে পরিলক্ষিত হয় যখন তারের একটি শাখা তার পথে উপস্থিত হয়। কন্ডাক্টরগুলি সমান্তরালভাবে সংযুক্ত হলে মোট বর্তমান শক্তির সূত্র:
I জেন=আমি 1 + আমি 2
যদি শাখাগুলি তার দিয়ে তৈরি হয়দুইটির বেশি, তাহলে উপরের সূত্রে একই সংখ্যা দ্বারা আরও পদ থাকবে।
স্ট্রেসের সূত্র
যখন একটি সার্কিট বিবেচনা করা হয় যেখানে কন্ডাক্টরগুলি সিরিজে সংযুক্ত থাকে, তখন সমগ্র বিভাগে ভোল্টেজ প্রতিটি নির্দিষ্ট প্রতিরোধকের এই মানের সমষ্টি দ্বারা নির্ধারিত হয়। আপনি প্লেট সঙ্গে এই পরিস্থিতি তুলনা করতে পারেন. একজন ব্যক্তির পক্ষে তাদের একটিকে ধরে রাখা সহজ হবে, তিনি দ্বিতীয়টিকে কাছাকাছি নিতেও সক্ষম হবেন, তবে অসুবিধার সাথে। একজন ব্যক্তি আর একে অপরের পাশে তিনটি প্লেট ধরে রাখতে সক্ষম হবে না, এক সেকেন্ডের সাহায্যের প্রয়োজন হবে। ইত্যাদি। মানুষের প্রচেষ্টা যোগ হয়।
পরিবাহীর সিরিজ সংযোগ সহ একটি সার্কিটের একটি অংশের মোট ভোল্টেজের সূত্রটি এইরকম দেখায়:
U gen=U 1 + U 2, যেখানে U পদটি গৃহীত হয় বৈদ্যুতিক ভোল্টেজের জন্য।
আরেকটি পরিস্থিতি দেখা দেয় যদি প্রতিরোধকের সমান্তরাল সংযোগ বিবেচনা করা হয়। যখন প্লেট একে অপরের উপরে স্ট্যাক করা হয়, তখনও সেগুলি একজন ব্যক্তি ধরে রাখতে পারে। তাই আপনাকে কিছু যোগ করতে হবে না। একই সাদৃশ্য পরিলক্ষিত হয় যখন কন্ডাক্টরগুলি সমান্তরালভাবে সংযুক্ত থাকে। তাদের প্রতিটির ভোল্টেজ একই এবং একই সময়ে তাদের সকলের ভোল্টেজের সমান। মোট ভোল্টেজের সূত্র হল:
U জেন=U1=U2
বৈদ্যুতিক প্রতিরোধের সূত্র
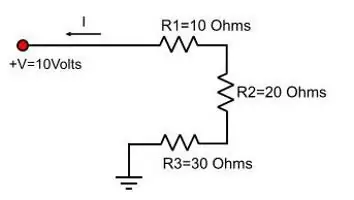
আপনি এগুলি আর মুখস্থ করতে পারবেন না, তবে ওহমের সূত্রের সূত্রটি জানুন এবং এটি থেকে পছন্দসইটি বের করুন। এটি এই আইন থেকে অনুসরণ করে যেভোল্টেজ বর্তমান এবং প্রতিরোধের গুণফলের সমান। অর্থাৎ, U=IR, যেখানে R হল রোধ।
তাহলে আপনাকে যে সূত্রটি দিয়ে কাজ করতে হবে তা নির্ভর করে কন্ডাক্টরগুলি কীভাবে সংযুক্ত রয়েছে তার উপর:
- সিরিজে, তাই ভোল্টেজের জন্য আপনার সমতা প্রয়োজন - IgenRমোট=I1R1 + I2R2;
- সমান্তরালে, বর্তমান শক্তির জন্য সূত্রটি ব্যবহার করা প্রয়োজন - Uমোট / Rমোট=U 1 / R1 + U2 / R2 .
সাধারণ রূপান্তর দ্বারা অনুসরণ করা হয়, যা এই সত্যের উপর ভিত্তি করে যে প্রথম সমতায় সমস্ত প্রবাহের মান একই, এবং দ্বিতীয়টিতে - ভোল্টেজগুলি সমান। তাই তাদের ছোট করা যেতে পারে। অর্থাৎ, নিম্নলিখিত অভিব্যক্তিগুলি পাওয়া যায়:
- R gen=R 1 + R 2 (কন্ডাক্টরের সিরিজ সংযোগের জন্য).
- 1 / R জেন=1 / R 1 + 1 / R 2(সমান্তরালভাবে সংযুক্ত হলে)।
যখন নেটওয়ার্কের সাথে সংযুক্ত প্রতিরোধকের সংখ্যা বৃদ্ধি পায়, তখন এই অভিব্যক্তিতে পদের সংখ্যা পরিবর্তিত হয়।
এটা লক্ষণীয় যে কন্ডাক্টরের সমান্তরাল এবং সিরিজ সংযোগ মোট প্রতিরোধের উপর আলাদা প্রভাব ফেলে। তাদের মধ্যে প্রথমটি সার্কিট বিভাগের প্রতিরোধকে হ্রাস করে। তদুপরি, এটি ব্যবহৃত প্রতিরোধকগুলির মধ্যে সবচেয়ে ছোট থেকে কম দেখা যাচ্ছে। সিরিজে সংযুক্ত হলে, সবকিছুই যৌক্তিক: মানগুলি যোগ করে, তাই মোট সংখ্যা সর্বদা সবচেয়ে বড় হবে।
কাজের বর্তমান
আগের তিনটি পরিমাণ একটি সার্কিটে সমান্তরাল সংযোগ এবং কন্ডাকটরগুলির সিরিজ বিন্যাসের নিয়ম তৈরি করে। অতএব, তাদের জানা অপরিহার্য। কাজ এবং ক্ষমতা সম্পর্কে, আপনি শুধুমাত্র মৌলিক সূত্র মনে রাখা প্রয়োজন. এটি নিম্নরূপ লেখা হয়েছে: A \u003d IUt, যেখানে A হল কারেন্টের কাজ, t হল কন্ডাকটরের মধ্য দিয়ে যাওয়ার সময়।
একটি সিরিয়াল সংযোগের সাথে মোট কাজ নির্ধারণ করার জন্য, আপনাকে মূল অভিব্যক্তিতে ভোল্টেজ প্রতিস্থাপন করতে হবে। আপনি সমতা পাবেন: A \u003d I(U 1 + U 2)t, বন্ধনী খুললে দেখা যাচ্ছে যে সমগ্র বিভাগে কাজ প্রতিটি নির্দিষ্ট বর্তমান ভোক্তার জন্য তাদের পরিমাণ সমান।
একটি সমান্তরাল সংযোগ স্কিম বিবেচনা করা হলে যুক্তি একইভাবে এগিয়ে যায়। শুধুমাত্র বর্তমান শক্তি প্রতিস্থাপন করা অনুমিত হয়. কিন্তু ফলাফল একই হবে: A=A 1 + A 2।
বর্তমান শক্তি
একটি সার্কিট বিভাগের পাওয়ার (স্বরলিপি "P") জন্য একটি সূত্র বের করার সময়, আপনাকে আবার একটি সূত্র ব্যবহার করতে হবে: P \u003d UI। এই ধরনের যুক্তির পরে, দেখা যাচ্ছে যে সমান্তরাল এবং সিরিজ সংযোগগুলি হল পাওয়ার জন্য এই ধরনের একটি সূত্র দ্বারা বর্ণিত: P \u003d P1 + P 2।
অর্থাৎ, স্কিমগুলি যেভাবেই তৈরি করা হোক না কেন, কাজের সাথে জড়িতদের মোট ক্ষমতা হবে। এটি ব্যাখ্যা করে যে একই সময়ে অ্যাপার্টমেন্ট নেটওয়ার্কে অনেকগুলি শক্তিশালী ডিভাইস অন্তর্ভুক্ত করা অসম্ভব। সে শুধু ভার নিতে পারে না।
কন্ডাক্টরের সংযোগ কীভাবে নববর্ষের মালা মেরামতকে প্রভাবিত করে?
একটি বাল্ব জ্বলে যাওয়ার পরপরই, তারা কীভাবে সংযুক্ত ছিল তা স্পষ্ট হয়ে যায়। এসিরিয়াল সংযোগ, তাদের কেউ আলোকিত হবে না. এটি এই কারণে যে একটি বাতি যা অব্যবহারযোগ্য হয়ে উঠেছে সার্কিটে একটি বিরতি তৈরি করে। অতএব, কোনটি পুড়ে গেছে তা নির্ধারণ করতে আপনাকে সবকিছু পরীক্ষা করতে হবে, এটি প্রতিস্থাপন করুন - এবং মালা কাজ শুরু করবে।
যদি এটি একটি সমান্তরাল সংযোগ ব্যবহার করে, তবে বাল্বগুলির একটি ব্যর্থ হলে এটি কাজ করা বন্ধ করে না। সব পরে, চেইন সম্পূর্ণরূপে ভাঙ্গা হবে না, কিন্তু শুধুমাত্র একটি সমান্তরাল অংশ। এই ধরনের মালা মেরামত করার জন্য, আপনাকে সার্কিটের সমস্ত উপাদান পরীক্ষা করতে হবে না, তবে শুধুমাত্র যেগুলি জ্বলছে না।
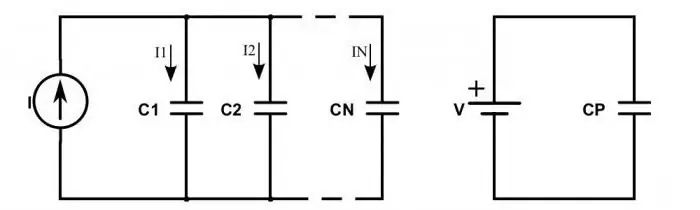
রোধকের পরিবর্তে ক্যাপাসিটর অন্তর্ভুক্ত করা হলে সার্কিটের কী হবে?
যখন তারা সিরিজে সংযুক্ত থাকে, নিম্নলিখিত পরিস্থিতি পরিলক্ষিত হয়: পাওয়ার উত্সের প্লাস থেকে চার্জ শুধুমাত্র চরম ক্যাপাসিটারের বাইরের প্লেটে আসে। এর মধ্যে যারা কেবল চেইন বরাবর সেই চার্জটি পাস করে। এটি ব্যাখ্যা করে যে সমস্ত প্লেটে একই চার্জ প্রদর্শিত হয়, কিন্তু বিভিন্ন চিহ্ন সহ। অতএব, সিরিজে সংযুক্ত প্রতিটি ক্যাপাসিটরের বৈদ্যুতিক চার্জ নিম্নরূপ লেখা যেতে পারে:
q জেন =q 1=q 2.
প্রতিটি ক্যাপাসিটরের ভোল্টেজ নির্ধারণ করতে, আপনাকে সূত্রটি জানতে হবে: U=q / C। এতে, C হল ক্যাপাসিটরের ক্যাপাসিট্যান্স।
মোট ভোল্টেজ প্রতিরোধক হিসাবে একই নিয়ম অনুসরণ করে। অতএব, ক্যাপাসিট্যান্স সূত্রে ভোল্টেজকে যোগফলের সাথে প্রতিস্থাপন করে, আমরা পাই যে ডিভাইসগুলির মোট ক্যাপাসিট্যান্স অবশ্যই সূত্র ব্যবহার করে গণনা করা উচিত:
C=q / (U 1 + U2)।
আপনি ভগ্নাংশ ফ্লিপ করে এবং ক্যাপাসিট্যান্সের সাথে চার্জের জন্য ভোল্টেজের অনুপাত প্রতিস্থাপন করে এই সূত্রটিকে সরল করতে পারেন। এটি নিম্নলিখিত সমতা দেখায়: 1 / С=1 / С 1 + 1 / С 2.
ক্যাপাসিটারগুলি সমান্তরালভাবে সংযুক্ত থাকলে পরিস্থিতি কিছুটা আলাদা দেখায়। তারপরে মোট চার্জ সমস্ত ডিভাইসের প্লেটে জমা হওয়া সমস্ত চার্জের যোগফল দ্বারা নির্ধারিত হয়। এবং ভোল্টেজ মান এখনও সাধারণ আইন অনুযায়ী নির্ধারিত হয়। অতএব, সমান্তরালভাবে সংযুক্ত ক্যাপাসিটরগুলির মোট ক্যাপাসিট্যান্সের সূত্র হল:
С=(q 1 + q 2) / U.
অর্থাৎ, এই মানটিকে সংযোগে ব্যবহৃত প্রতিটি ডিভাইসের যোগফল হিসাবে বিবেচনা করা হয়:
S=S1 + S2.
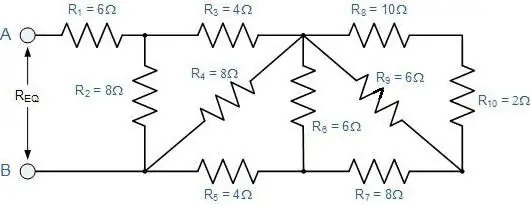
কন্ডাক্টরের নির্বিচারে সংযোগের মোট রোধ কীভাবে নির্ধারণ করবেন?
অর্থাৎ, যার মধ্যে ধারাবাহিক বিভাগগুলি সমান্তরাল অংশগুলিকে প্রতিস্থাপন করে এবং এর বিপরীতে। তাদের জন্য, সমস্ত বর্ণিত আইন এখনও বৈধ। শুধুমাত্র আপনাকে সেগুলি ধাপে ধাপে প্রয়োগ করতে হবে।
প্রথম, এটি মানসিকভাবে স্কিমটি প্রসারিত করার কথা। যদি এটি কল্পনা করা কঠিন হয়, তাহলে আপনাকে কী ঘটবে তা আঁকতে হবে। ব্যাখ্যাটি আরও পরিষ্কার হয়ে যাবে যদি আমরা এটিকে একটি নির্দিষ্ট উদাহরণ দিয়ে বিবেচনা করি (চিত্র দেখুন)।
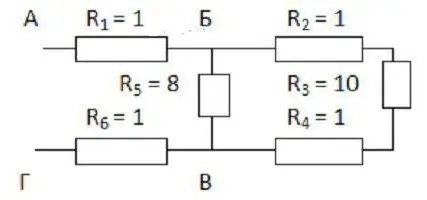
বি এবং সি বিন্দু থেকে অঙ্কন শুরু করা সুবিধাজনক। এগুলিকে একে অপরের থেকে এবং শীটের প্রান্ত থেকে কিছু দূরত্বে স্থাপন করতে হবে। বাম দিকে, একটি তার বিন্দুর কাছে পৌঁছেছে এবং দুটি ইতিমধ্যেই ডানদিকে নির্দেশিত হয়েছে। অন্যদিকে বিন্দু বিন্দুর বাম দিকে দুটি শাখা রয়েছে এবং এর পরে একটি তার রয়েছে।
এখন আপনাকে এইগুলির মধ্যে স্থান পূরণ করতে হবেবিন্দু 2, 3 এবং 4 সহগ সহ তিনটি প্রতিরোধক উপরের তারের সাথে স্থাপন করা উচিত এবং 5 এর সূচক সহ একটি নীচে থেকে যাবে। প্রথম তিনটি সিরিজে সংযুক্ত রয়েছে। পঞ্চম প্রতিরোধকের সাথে তারা সমান্তরালে রয়েছে।
বাকি দুটি প্রতিরোধক (প্রথম এবং ষষ্ঠ) বিভির বিবেচিত অংশের সাথে সিরিজে সংযুক্ত। অতএব, অঙ্কনটি কেবল নির্বাচিত পয়েন্টগুলির উভয় পাশে দুটি আয়তক্ষেত্রের সাথে সম্পূরক হতে পারে। প্রতিরোধের গণনা করার জন্য সূত্রগুলি প্রয়োগ করা বাকি আছে:
- প্রথমটি সিরিয়াল সংযোগের জন্য দেওয়া হয়েছে;
- তারপর সমান্তরাল জন্য;
- এবং আবার পরপর।
এইভাবে, আপনি যেকোনো, এমনকি খুব জটিল স্কিম স্থাপন করতে পারেন।
পরিবাহীর সিরিয়াল সংযোগের সমস্যা
শর্ত। দুটি বাতি এবং একটি প্রতিরোধক একটি সার্কিটে একটির পিছনে আরেকটি সংযুক্ত থাকে। মোট ভোল্টেজ হল 110 V এবং কারেন্ট হল 12 A। প্রতিটি ল্যাম্পকে 40 V রেট দেওয়া হলে রোধের মান কত?
সিদ্ধান্ত। যেহেতু একটি সিরিজ সংযোগ বিবেচনা করা হচ্ছে, তার আইনগুলির সূত্রগুলি জানা যায়৷ আপনি শুধু সঠিকভাবে তাদের প্রয়োগ করতে হবে. প্রতিরোধক জুড়ে ভোল্টেজের মান খুঁজে বের করে শুরু করুন। এটি করার জন্য, আপনাকে মোট থেকে একটি প্রদীপের ভোল্টেজের দুই গুণ বিয়োগ করতে হবে। দেখা যাচ্ছে 30 V.
এখন যেহেতু দুটি পরিমাণ জানা গেছে, U এবং I (তাদের দ্বিতীয়টি শর্তে দেওয়া হয়েছে, যেহেতু প্রতিটি সিরিজের ভোক্তার মোট কারেন্ট কারেন্টের সমান), আমরা ব্যবহার করে রোধের রোধ গণনা করতে পারি ওম এর আইন. এটি 2.5 ওহম হতে দেখা যাচ্ছে।
উত্তর। রোধের রোধ 2.5 ওহম।
টাস্কক্যাপাসিটর, সমান্তরাল এবং সিরিজের সংযোগের জন্য
শর্ত। 20, 25 এবং 30 মাইক্রোফ্যারাডের ক্ষমতা সহ তিনটি ক্যাপাসিটার রয়েছে। সিরিজ এবং সমান্তরালে সংযুক্ত হলে তাদের মোট ক্যাপাসিট্যান্স নির্ধারণ করুন।
সিদ্ধান্ত। একটি সমান্তরাল সংযোগ দিয়ে শুরু করা সহজ। এই পরিস্থিতিতে, সমস্ত তিনটি মান যোগ করা প্রয়োজন। এইভাবে, মোট ক্যাপাসিট্যান্স হল 75uF।
এই ক্যাপাসিটারগুলি সিরিজে সংযুক্ত হলে গণনাগুলি কিছুটা জটিল হবে৷ সর্বোপরি, প্রথমে আপনাকে এই প্রতিটি ক্ষমতার সাথে একতার অনুপাত খুঁজে বের করতে হবে এবং তারপর একে অপরের সাথে যুক্ত করতে হবে। দেখা যাচ্ছে যে মোট ক্ষমতা দ্বারা ভাগ করা একক হল 37/300। তাহলে কাঙ্খিত মান হল আনুমানিক ৮ মাইক্রোফ্যারাড।
উত্তর। সিরিজ সংযোগে মোট ক্যাপাসিট্যান্স 8 uF, সমান্তরালে - 75 uF।






