পদার্থের গ্যাসীয় সামগ্রিক অবস্থার তাপগতিবিদ্যা হল পদার্থবিদ্যার একটি গুরুত্বপূর্ণ শাখা যা সিস্টেমে তাপগতিগত ভারসাম্য এবং আধা-স্থির পরিবর্তনগুলি অধ্যয়ন করে। প্রধান মডেল যার উপর ভিত্তি করে সিস্টেমের আচরণের ভবিষ্যদ্বাণী করা হয় তা হল আদর্শ গ্যাস মডেল। এর ব্যবহারের সাথে, মেন্ডেলিভ-ক্লেপিরন সমীকরণ প্রাপ্ত হয়েছিল। নিবন্ধে এটি বিবেচনা করুন।
আদর্শ গ্যাস
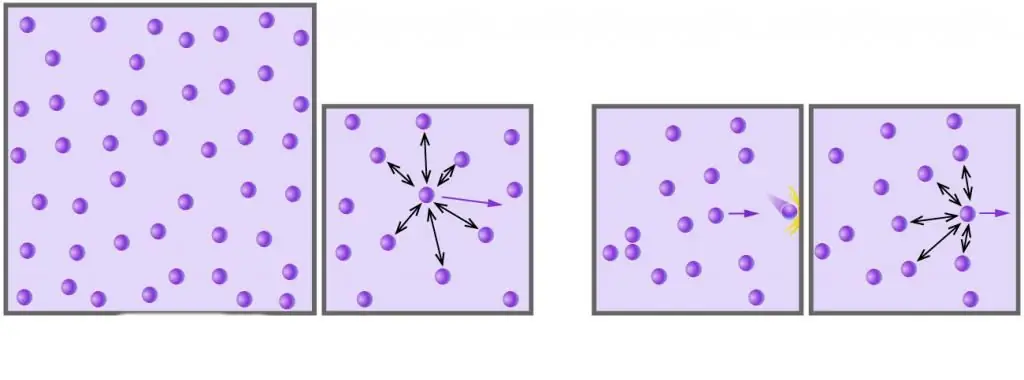
আপনি জানেন, সমস্ত বাস্তব গ্যাস অণু বা পরমাণু নিয়ে গঠিত, যার মধ্যে দূরত্ব কম চাপে তাদের আকারের তুলনায় অনেক বেশি। উপরন্তু, উচ্চ তাপমাত্রায়, পরম স্কেলে, অণুর গতিশক্তি দুর্বল ডাইপোল-ডাইপোল মিথস্ক্রিয়াগুলির সাথে যুক্ত তাদের সম্ভাব্য শক্তিকে ছাড়িয়ে যায় (যদি, এই মিথস্ক্রিয়াগুলি ছাড়াও, অন্যান্য ধরণের রাসায়নিক বন্ধন থাকে, উদাহরণস্বরূপ, আয়নিক বা হাইড্রোজেন, তারপর তারা অভ্যন্তরীণ সিস্টেম শক্তির সম্ভাব্য উপাদানে একটি গুরুত্বপূর্ণ অবদান রাখে)।
কারণস্বাভাবিকের কাছাকাছি পরিস্থিতিতে অনেক বাস্তব গ্যাসের জন্য, কেউ তাদের অভ্যন্তরীণ মিথস্ক্রিয়া এবং কণার আকারকে অবহেলা করতে পারে। এই দুটি প্রধান অনুমান আদর্শ গ্যাস মডেল গঠন করে৷
পদার্থবিজ্ঞানে মেন্ডেলিভের সমীকরণ

এই সমীকরণটিকে ক্ল্যাপেয়ারন-মেন্ডেলিভ আইন বলা আরও সঠিক এবং ন্যায্য। ঘটনাটি হল যে এটি প্রথম 1834 সালে ফরাসি প্রকৌশলী এমিল ক্ল্যাপেয়ারন দ্বারা রেকর্ড করা হয়েছিল। তিনি 19 শতকের শুরুতে আবিষ্কৃত বয়েল-ম্যারিওট, গে-লুসাক এবং চার্লসের গ্যাস আইন বিশ্লেষণ করে এটি করেছিলেন।
রাশিয়ান রসায়নবিদ দিমিত্রি মেন্ডেলিভের যোগ্যতা এই যে তিনি সমীকরণটিকে একটি আধুনিক এবং সহজে ব্যবহারযোগ্য গাণিতিক রূপ দিয়েছেন। বিশেষ করে, মেন্ডেলিভ সমীকরণে সমস্ত গ্যাসের জন্য একটি ধ্রুবক R=8, 314 J/(molK) প্রবর্তন করেছিলেন। ক্ল্যাপেয়ারন নিজে বেশ কিছু অভিজ্ঞতামূলক ধ্রুবক ব্যবহার করেছেন যা গণনা প্রক্রিয়াকে কঠিন করে তোলে।
মেন্ডেলিভ-ক্লেপিরন সমীকরণটি নিম্নরূপ লেখা হয়েছে:
PV=nRT.
এই সমতার অর্থ হল এক্সপ্রেশনের বাম দিকে চাপ P এবং ভলিউম V এর গুণফল সর্বদা পরম তাপমাত্রা T এর গুণফল এবং বাম দিকে n পদার্থের পরিমাণের সমানুপাতিক।
অধ্যয়নের অধীনে অভিব্যক্তিটি আপনাকে গ্যাস আইন পেতে অনুমতি দেয় যদি আপনি এর চারটি প্যারামিটারের মধ্যে দুটি ঠিক করেন। আইসোপ্রসেসের ক্ষেত্রে, বদ্ধ সিস্টেমগুলি অধ্যয়ন করা হয় যেখানে পরিবেশের সাথে পদার্থের কোনও বিনিময় নেই (n=const)। এই প্রক্রিয়াগুলি একটি একক স্থির থার্মোডাইনামিক প্যারামিটার (T, P বা V) দ্বারা চিহ্নিত করা হয়।

উদাহরণ সমস্যা
এবার মেন্ডেলিভ-ক্লেপিরন সমীকরণের সমস্যাটি সমাধান করা যাক। এটি জানা যায় যে 500 গ্রাম ওজনের অক্সিজেন 2 বায়ুমণ্ডলের চাপে 100 লিটারের আয়তনের একটি সিলিন্ডারে থাকে। সিস্টেমটি থার্মোডাইনামিক ভারসাম্যের প্রেক্ষিতে বেলুনের তাপমাত্রা কত।
স্মরণ করুন যে, সংজ্ঞা অনুসারে, একটি পদার্থের পরিমাণ সূত্র দ্বারা গণনা করা হয়:
n=m/M.
যেখানে m হল সিস্টেমের সমস্ত কণার ভর, M হল তাদের গড় মোলার ভর। এই সমতা আমাদের নিম্নলিখিত আকারে মেন্ডেলিভ সমীকরণটি পুনরায় লেখার অনুমতি দেয়:
PV=mRT/M.
যেখানে আমরা এই কাজের জন্য কার্যকরী সূত্র পাব:
T=PVM/(mR)।
এটি সমস্ত পরিমাণকে এসআই ইউনিটে রূপান্তর করতে এবং তাদের এই রাশিতে প্রতিস্থাপন করতে রয়ে গেছে:
T=21013250, 10, 032/(0, 58, 314)=156 K.
গণনা করা তাপমাত্রা হল -117 oC। যদিও এই তাপমাত্রায় অক্সিজেন এখনও বায়বীয় (এটি -182.96 oC এ ঘনীভূত হয়), এই ধরনের পরিস্থিতিতে আদর্শ গ্যাস মডেল শুধুমাত্র গণনা করা মানের একটি গুণগত অনুমান পেতে ব্যবহার করা যেতে পারে।






